John E. Howland
Department of Computer Science
Trinity University
715 Stadium Drive
San Antonio, Texas 78212-7200
Voice: (210) 999-7364
Fax: (210) 999-7477
E-mail: jhowland@Ariel.CS.Trinity.Edu
Web: http://WWW.CS.Trinity.Edu/~jhowland/
October 24, 2005
Subject Areas: Computer Graphics.
Keywords: 2D Viewing, 3D Viewing, modeling, linear algebra.
Computer graphics deals with the problem of image synthesis. Given a model (usually mathematically based) the problem of computer graphics is to produce realistic image data which may be viewed on a graphics display device. The process of producing the image data from the scene model is called rendering. That images are synthesized from mathematical models implies that computer graphics is a mathematcally based subject. Image synthesis involves the physics of light, properties of materials, etc. Animated imagery involves simulation theory, finite element analysis, kinematics, sampling theory and other mathmatically based fields. The study of computer graphics necessarily involves the study of many areas of mathematics. In the following sections we give an elementary view of some of these topics. Students who have an interest in computer graphics should study as much mathematics as possible.
The reverse problem of starting with image data and recovering information is called image processing.
We now consider the problem of representing 2D graphics images
which may be drawn as a sequence of connected line segments. Such images
may be represented as a matrix of 2D points
![]() .
.
The J programming notation [Hui 2001] is used to describe the viewing transformations and data object representations.
For example:
[ square =: 5 2 $ 0 0 10 0 10 10 0 10 0 0 0 0 10 0 10 10 0 10 0 0
represents the square shown in Figure 1
The idea behind this representation is that the first point represents
the starting point of the first line segment drawn while the second
point represents the end of the first line segment and the starting
point of the second line segment. The drawing of line segments continues
in similar fashion until all line segments have been drawn. A
matrix having ![]() points describes a figure consisting of
points describes a figure consisting of ![]() line segments. It is sometimes useful to think of each pair of consecutive
points in this matrix representation,
line segments. It is sometimes useful to think of each pair of consecutive
points in this matrix representation,
as as a vector so that the square shown in Figure 1 is the result of drawing the vectors shown in Figure 2.
Suppose we wish to rotate a figure around the origin of our 2D coordinate
system. Figure 3 shows the point
![]() being rotated
being rotated ![]() degrees (by convention, counter clock-wise direction
is positive) about the origin.
degrees (by convention, counter clock-wise direction
is positive) about the origin.
The equations for changes in the ![]() and
and ![]() coordinates are:
coordinates are:
If we consider the coordinates of the point ![]() as a one row
two column matrix
as a one row
two column matrix
![]() and the matrix
and the matrix
then, given the J definition for matrix product, mp =: +/ . *,
we can write Equations (1) as the matrix equation
We can define a J monad, rotate, which produces the
rotation matrix. This monad is applied to an angle, expressed
in degrees. Positive angles are measured in a counter-clockwise
direction by convention.
rotate =: monad def '2 2 $ 1 1 _1 1 * 2 1 1 2 o. (o. y.) % 180'
rotate 90
0 1
_1 0
rotate 360
1 _2.44921e_16
2.44921e_16 1
We can rotate the square of Figure 1 by:
square mp rotate 90 0 0 0 10 _10 10 _10 0 0 0
producing the square shown in Figure 4.
Next we consider the problem of scaling (changing the size of) a 2D line drawing.
Size changes are always made from the origin of the coordinate system.
The equations for changes in the ![]() and
and ![]() coordinates are:
coordinates are:
As before, we consider the coordinates of the point ![]() as a one row
two column matrix
as a one row
two column matrix
![]() and the matrix
and the matrix
then, we can write Equations (3) as the matrix equation
We next define a J monad, scale, which produces the scale matrix. This
monad is applied to a list of two scale factors for ![]() and
and ![]() respectively.
respectively.
scale =: monad def '2 2 $ (0 { y.),0,0,(1 { y.)'
scale 2 3
2 0
0 3
We can now scale the square of Figure 1 by:
square mp scale 2 3 0 0 20 0 20 30 0 30 0 0
producing the rectangle shown in Figure 5.
The third 2D graphics transformation we consider is that of translating
a 2D line drawing by an amount ![]() along the
along the ![]() axis and
axis and ![]() along
the
along
the ![]() axis. The translation equations may be written as:
axis. The translation equations may be written as:
We wish to write the Equations 5 as a single matrix equation. This requires that we find a 2 by 2 matrix,
such that
![]() . From this it is
clear that
. From this it is
clear that ![]() and
and ![]() , but there is no way to obtain the
, but there is no way to obtain the
![]() term required in the first equation of Equations 5.
Similarly we must have
term required in the first equation of Equations 5.
Similarly we must have
![]() . Therefore,
. Therefore,
![]() and
and ![]() , and there is no way to obtain the
, and there is no way to obtain the
![]() term required in the second equation of Equations 5.
term required in the second equation of Equations 5.
To summarize, we inject the 2D plane into 3 space by the mapping
Then we solve our problem, ensuring that our solution lies in the
plane ![]() . Our final answer is obtained by the projection of the
plane
. Our final answer is obtained by the projection of the
plane ![]() on 2 space by the mapping
on 2 space by the mapping
This process is referred to as using homogeneous coordinates. In the context
of our problem (finding matrix representations of rotation, scaling and
translation transformations) we must inject our 2D line drawings into
the plane ![]() . In J we do this by using
. In J we do this by using stitch, ,..
square ,. 1 0 0 1 10 0 1 10 10 1 0 10 1 0 0 1
We now must rewrite the Equations 5 as
Consider the 3 by 3 matrix
![\begin{displaymath}
\left[
\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
T_x & T_y & 1
\end{array}\right]
\end{displaymath}](img38.gif)
We now see that the Equations 8 may be written as the matrix equation
We define the J monad translate, which is applied to a list of
two translate values
![]() .
.
translate =: monad def '3 3 $ 1 0 0 0 1 0 , y. , 1' translate 10 _10 1 0 0 0 1 0 10 _10 1
We translate the square of Figure 1 by
(square ,. 1) mp translate 10 _10 10 _10 1 20 _10 1 20 0 1 10 0 1 10 _10 1
Notice that the translate matrix (having a last column 0 0 1) always produces
a result which lies in the plane ![]() . We can perform the translation operation
and project the result back on the 2D plane (saving computation time by not
doing unnecessary multiplications and additions) by
. We can perform the translation operation
and project the result back on the 2D plane (saving computation time by not
doing unnecessary multiplications and additions) by
(square ,. 1) mp 3 2 {. translate 10 _10
10 _10
20 _10
20 0
10 0
10 _10
producing the translated square shown in Figure 6
We want to be able to combine sequences of rotations, scaling and translations together as a single 2D graphics transformation. We accomplish this by simply multiplying the matrix representations of each transformation using matrix multiplication. However, to do this, we must go back and rewrite the Equations 1 and 3 as the following:
Similarly we rewrite the matrix Equations 2 and 4 as:
We extend our earlier J definitions of rotate and scale to the
homogenous coordinate system.
rotate =: monad def '((2 2 $ 1 1 _1 1 * 2 1 1 2 o. (o. y.) % 180),.0),0 0 1'
rotate 180
_1 0 0
0 _1 0
0 0 1
(square ,. 1) mp 3 2 {. rotate 180
0 0
_10 0
_10 _10
0 _10
0 0
scale =: monad def '3 3 $ (0 { y.), 0 0 0 , (1 { y.), 0 0 0 1'
scale 2 3
2 0 0
0 3 0
0 0 1
(square ,. 1) mp 3 2 {. scale 2 3
0 0
20 0
20 30
0 30
0 0
Figure 5 shows the resulting scaled square.
We can now combine together two transformations to form a single graphics
operation. For example, suppose we wish to first rotate an object 90 degrees
and then scale the object by 2 along the ![]() axis.
axis.
The rotation would be expressed as:
[r =: rotate 90
0 1 0
_1 0 0
0 0 1
Then the scaling operation would be expressed as:
[s =: scale 2 1 2 0 0 0 1 0 0 0 1
Applying these operations to the square, we have:
(((square ,. 1) mp 3 2 {. r) ,. 1) mp 3 2 {. s
0 0
0 10
_20 10
_20 0
0 0
However, notice that
(square ,. 1) mp 3 2 {. r mp s
0 0
0 10
_20 10
_20 0
0 0
produces the same result using far fewer multiplications and additions. Figure 8 shows the rotated and scaled square.
We are allowed to perform the matrix multiplications of r and s before
multiplying by square ,. 1 because matrix multiplication is associative.
Be careful! Matrix multiplication is not commumative.
r mp s 0 1 0 _2 0 0 0 0 1 s mp r 0 2 0 _1 0 0 0 0 1
This means we must be careful about the order of application of graphics transformations.
One might be concerned about whether or not multiplying rotation, scaling and/or
translation matrices produces a transformation which leaves our 2D lines in the
plane ![]() . We can answer this question by observing that each of these matrices
has a last column of
. We can answer this question by observing that each of these matrices
has a last column of
![]() . Hence, when multiplying
any two of these matrices, the product matrix has a last
column of
. Hence, when multiplying
any two of these matrices, the product matrix has a last
column of
![]() .
.
As a final example, suppose we wish to rotate the square of Figure 1
90 degrees about its upper right corner. We must first translate the point
![]() to the origin. This is the matrix
to the origin. This is the matrix
translate _10 _10 1 0 0 0 1 0 _10 _10 1
Then we must rotate 90 degrees
rotate 90 0 1 0 _1 0 0 0 0 1
Finally, we translate the square back with the matrix
translate 10 10 1 0 0 0 1 0 10 10 1
Putting this all together we have:
[xform =: (translate _10 _10) mp (rotate 90) mp translate 10 10
0 1 0
_1 0 0
20 0 1
(square ,. 1) mp 3 2 {. xform
20 0
20 10
10 10
10 0
20 0
which is shown in Figure 9.
Three dimensional objects may be modeled by a collection of points ![]() , representing
the vertices of the object, together with additional information which describes which vertices are
used to form planes, surface properties such as color and texture, etc. Such an image model is
often refered to as a polygonal model.
, representing
the vertices of the object, together with additional information which describes which vertices are
used to form planes, surface properties such as color and texture, etc. Such an image model is
often refered to as a polygonal model.
For example, the vertices of a cube of size 2, centered at the origin of three-dimensional space can be generated by:
[ cube =: _1 ^ #: i. 8 1 1 1 1 1 _1 1 _1 1 1 _1 _1 _1 1 1 _1 1 _1 _1 _1 1 _1 _1 _1
The top plane of this cube are describe by vertices 0 1 5 4.
0 1 5 4 { cube
1 1 1
1 1 _1
_1 1 _1
_1 1 1
The five other planes in this cube are similarly described. For example, the left face is given by
4 5 7 6 { cube
_1 1 1
_1 1 _1
_1 _1 _1
_1 _1 1
The 2D transformations of Section 5.1 may be extended to the 3D case as follows.
Using homogeneous coordinates we extend the Equations 8 to three dimensional space:
Consider the 4 by 4 matrix
![\begin{displaymath}
\left[
\begin{array}{llll}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 0\\
T_x & T_y & T_z & 1
\end{array}\right]
\end{displaymath}](img53.gif)
We see that the Equations 14 may be written as the matrix equation
We define the J monad translate which is applied to a list of
three translate values
![]() to produce the translation matrix.
to produce the translation matrix.
translate =: monad def '((=/ ~ i. 3) , y. ) ,. 0 0 0 1' translate 1 1 1 1 0 0 0 0 1 0 0 0 0 1 0 1 1 1 1
Hence,
(cube ,. 1) mp 4 3 {. translate 1 1 1
2 2 2
2 2 0
2 0 2
2 0 0
0 2 2
0 2 0
0 0 2
0 0 0
translates the cube to the positive sector of 3-space.
Next we extend the Equations 3 to three dimensional space as the follows:
Consider the 4 by 4 matrix
![\begin{displaymath}
\left[
\begin{array}{llll}
S_x & 0 & 0 & 0\\
0 & S_y & 0 & 0\\
0 & 0 & S_z & 0\\
0 & 0 & 0 & 1
\end{array}\right]
\end{displaymath}](img57.gif)
We write the Equations 16 as:
We define the J monad scale which is applied to a list of three
scale factors
![]() to produce
the scaling matrix.
to produce
the scaling matrix.
scale =: monad def '4 4 $ (0 { y.), 0 0 0 0 , (1 { y.), 0 0 0 0 , (2 { y.), 0 0 0 0 1'
We can scale cube to size 4 by:
(cube ,. 1) mp 4 3 {. scale 2 2 2
2 2 2
2 2 _2
2 _2 2
2 _2 _2
_2 2 2
_2 2 _2
_2 _2 2
_2 _2 _2
Extending the Equations 1 to three dimensional space
is a bit more complex as we need to describe three rotation matrices which
rotate points about the ![]() ,
, ![]() , and
, and ![]() axes respectively.
axes respectively.
The ![]() axis rotation equations are:
axis rotation equations are:
Consider the 4 by 4 matrix
![\begin{displaymath}
\left[
\begin{array}{rrrr}
cos(\theta) & sin(\theta) & 0 & 0...
...) & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1
\end{array}\right]
\end{displaymath}](img62.gif)
We write Equations 18 as:
We define the J monad z_rotate which is applied to an angle ![]() to
produce the
to
produce the ![]() axis rotation matrix.
axis rotation matrix.
z_rotate =: monad def '(1 1 _1 1 * 2 1 1 2 o. (o. y.) % 180) (0 0;0 1;1 0;1 1) } =/ ~ i. 4' z_rotate 90 0 1 0 0 _1 0 0 0 0 0 1 0 0 0 0 1
We can rotate cube 90 degrees about the ![]() axis by
axis by
(cube ,. 1) mp 4 3 {. z_rotate 90
_1 1 1
_1 1 _1
1 1 1
1 1 _1
_1 _1 1
_1 _1 _1
1 _1 1
1 _1 _1
We can also see that rotating the top face of cube
produces the left face of cube described in
Section 9
(0 1 5 4 { cube ,. 1) mp 4 3 {. z_rotate 90
_1 1 1
_1 1 _1
_1 _1 _1
_1 _1 1
The ![]() axis rotation equations are:
axis rotation equations are:
Consider the 4 by 4 matrix
![\begin{displaymath}
\left[
\begin{array}{rrrr}
cos(\theta) & 0 & - sin(\theta) &...
...eta) & 0 & cos(\theta) & 0\\
0 & 0 & 0 & 1
\end{array}\right]
\end{displaymath}](img65.gif)
We write Equations 20 as:
We define the J monad y_rotate which is applied to an angle ![]() to
produce the
to
produce the ![]() axis rotation matrix.
axis rotation matrix.
y_rotate =: monad def '(1 _1 1 1 * 2 1 1 2 o. (o. y.) % 180) (0 0;0 2;2 0;2 2) } =/ ~ i. 4' y_rotate 90 0 0 _1 0 0 1 0 0 1 0 0 0 0 0 0 1
We can rotate cube 90 degrees about the ![]() axis by
axis by
(cube ,. 1) mp 4 3 {. y_rotate 90
1 1 _1
_1 1 _1
1 _1 _1
_1 _1 _1
1 1 1
_1 1 1
1 _1 1
_1 _1 1
The ![]() axis rotation equations are:
axis rotation equations are:
Consider the 4 by 4 matrix
![\begin{displaymath}
\left[
\begin{array}{rrrr}
1 & 0 & 0 & 0\\
0 & cos(\theta) ...
...(\theta) & cos(\theta) & 0\\
0 & 0 & 0 & 1
\end{array}\right]
\end{displaymath}](img68.gif)
We write Equations 22 as:
We define the J monad x_rotate which is applied to an angle ![]() to
produce the
to
produce the ![]() axis rotation matrix.
axis rotation matrix.
x_rotate =: monad def '(1 1 _1 1 * 2 1 1 2 o. (o. y.) % 180) (1 1;1 2;2 1;2 2) } =/ ~ i. 4' x_rotate 90 1 0 0 0 0 0 1 0 0 _1 0 0 0 0 0 1
We can rotate cube 90 degrees about the ![]() axis by
axis by
(cube ,. 1) mp 4 3 {. x_rotate 90
1 _1 1
1 1 1
1 _1 _1
1 1 _1
_1 _1 1
_1 1 1
_1 _1 _1
_1 1 _1
The initial viewing parameters are choosen so as to be able to give an unrestricted view of the scene. In practice, however, some simplifications are most often used as default viewing parameters.
The projection plane, shown in Figure 10, has the view plane defined by a point on the plane (VRP) and the view plane normal (VPN).
The VPN gives the orientation of the view plane and is often (but not required to be) parallel to the view direction. The VPN is used to define a left-handed coordinate system screen coordinate system. The VUP vector defines a direction which is not parallel to VPN and is taken to be the viewer's concept of up. VUP need not (but often is taken to) be perpendicular to VPN. The projection of VUP on the view plane defines the V axis of the screen coordinate system. The U axis of the screen coordinate system is choosen to be perpendicular to both (orthogonal to) V and VPN. These vectors are choosen so as to form a left-handed V, U, VPN 3D coordinate system. The VRP is the origin of the 2D screen coordinate system. However, VRP is not the origin of the left-handed 3D coordinate system we wish to define. Its origin is the location of the eye (COP). The coordinates of COP are defined relative to the VRP using world coordinates.
We now have all of the parameters necessary to describe the 3D viewing transformation which maps the world coordinate system into the eye coordinate system. A rectangular region, Figure 11, (viewport) describes the clipping region of the screen coordinate system which is visible to the viewer.
This 2 dimensional viewport has sides which are parallel to the V U axis and the location and size of the viewport are given in units of the screen coordinate system using VRP as the origin. The viewport forms a viewing pyramid which gives the visible portion of world coordinate space from COP. All objects outside this pyramid are clipped from the scene. Actually, two additional clipping planes (Near and Far; see Figure 12) which are parallel to the view plane define portions of the seen which are either too close or too far from COP to be seen. The line from the COP through the center of the viewport defines the viewing direction and will be the positive Z axis of the eye coordinate system.
A few concepts from elementary linear algebra are useful
at this point. Let
![]() and
and
![]() be two
3D vectors. The dot product or inner product of
be two
3D vectors. The dot product or inner product of ![]() and
and ![]() is
defined as:
is
defined as:
Notice that the inner product of two vectors is a real number. The cosine of the
acute angle ![]() between two vectors
between two vectors ![]() and
and ![]() is defined
as:
is defined
as:
where
![]() is the length of the vector
is the length of the vector ![]() and
and
![]() is the length of the vector
is the length of the vector ![]() . Hence we may
write:
. Hence we may
write:
Notice that if ![]() and
and ![]() are two perpendicular vectors,
then the angle between each other is
are two perpendicular vectors,
then the angle between each other is ![]() and
and
![]() . Hence,
the inner product of two perpendicular vectors is
. Hence,
the inner product of two perpendicular vectors is ![]() .
.
The length of a vector
![]() is defined as
is defined as
![]() . The inner product of
. The inner product of ![]() with itself yields:
with itself yields:
or
If
![]() , then
, then
![]() .
.
Given two vectors
![]() and
and
![]() ,
then the sum of
,
then the sum of ![]() and
and ![]() is the vector
is the vector
which is shown in Figure 13.
Inner product (dot product) distributes over vector addition. That is,
given vectors ![]() ,
, ![]() ,
, ![]() , and a real
number
, and a real
number ![]() , then
, then
Suppose ![]() is a vector whose length is 1 and
is a vector whose length is 1 and ![]() is a vector not
parallel to
is a vector not
parallel to ![]() . We wish to project
. We wish to project ![]() to a vector
to a vector ![]() which lies on a plane perpendicular to
which lies on a plane perpendicular to ![]() (see Figure 14).
(see Figure 14).
To solve this problem define the vector ![]() by the equation:
by the equation:
Then,
But
![]() since
since ![]() is of length one. Hence,
is of length one. Hence,
![]() and from this it follows that
and from this it follows that ![]() and
and ![]() are perpendicular. Therefore,
are perpendicular. Therefore, ![]() is a vector that lies on a plane perpendicular
to
is a vector that lies on a plane perpendicular
to ![]()
The cross product of two vectors
![]() and
and
![]() is the vector:
is the vector:
The cross product of two non-parallel vectors is a vector which is perpendicular
to both vectors. Hence, the inner product of either ![]() or
or ![]() with
with
![]() is zero.
is zero.
The direction of the vector
![]() is such that if
the fingers of the right hand are curled around
is such that if
the fingers of the right hand are curled around ![]() in the direction of
in the direction of
![]() , then
, then
![]() is pointing in the direction
of the thumb. Cross product is not commutative.
is pointing in the direction
of the thumb. Cross product is not commutative.
which means that the direction of
![]() is the opposite
of the direction of
is the opposite
of the direction of
![]() .
.
The 3-D viewing pipline is shown in Figure 15. The second step of the
pipeline involves transforming the vertices of model objects which are given in world
coordinates to the eye coordinate system. This process starts from the initial
parameters of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . These vectors are first used to compute the
. These vectors are first used to compute the
![]() coordinate system as:
coordinate system as:
The next step is to transform the left-handed eye coordinate system defined by
![]() ,
, ![]() and
and ![]() into the right-handed world coordinate system.
This is accomplished by three steps:
into the right-handed world coordinate system.
This is accomplished by three steps:
The matrices required to accomplish this transformation are given next.
Since the center of projection, ![]() is defined relative to the
is defined relative to the ![]() , the translation
matrix is:
, the translation
matrix is:
![\begin{displaymath}
T = \left[
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 ...
...) & -(VRP[y]+COP[y]) & -(VRP[z]+COP[z]) & 1
\end{array}\right]
\end{displaymath}](img118.gif)
The rotation matrix is
![\begin{displaymath}
R = \left[
\begin{array}{cccc}
\mathbf{u}[x] & \mathbf{v}[x]...
...athbf{v}[z] & -VPN[z] & 0 \\
0 & 0 & 0 & 1
\end{array}\right]
\end{displaymath}](img119.gif)
The matrix to change the direction of the z-axis is
![\begin{displaymath}
C = \left[
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & -1 & 0 \\
0 & 0 & 0 & 1 \\
\end{array}\right]
\end{displaymath}](img120.gif)
We can combine the matrices ![]() and
and ![]() by computing the matrix product
by computing the matrix product ![]() and rename it
and rename it ![]() producing the matrix
producing the matrix
![\begin{displaymath}
R = \left[
\begin{array}{cccc}
\mathbf{u}[x] & \mathbf{v}[x]...
...mathbf{v}[z] & VPN[z] & 0 \\
0 & 0 & 0 & 1
\end{array}\right]
\end{displaymath}](img124.gif)
The final matrix to produce the transformation from world coordinates
to eye coordinates is the product of the two matrices
![]() .
.
After multiplying world coordinate vertices by the viewing transformation, ![]() ,
and clipping to the truncated viewing pyramid, it is necessary to perform
the perspective projection onto the view plane. Given a vertex in the eye coordinate
system,
,
and clipping to the truncated viewing pyramid, it is necessary to perform
the perspective projection onto the view plane. Given a vertex in the eye coordinate
system,
![]() , the projected screen coordinates,
, the projected screen coordinates,
![]() are computed as:
are computed as:
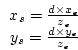
where ![]() is the distance from
is the distance from ![]() to the view plane. These formulas
are easily derived by considering the projection onto the
to the view plane. These formulas
are easily derived by considering the projection onto the ![]() (Figure
16) and
(Figure
16) and
![]() planes and noting that from similar triangles
planes and noting that from similar triangles
The equation for ![]() is derived in a similar fashion.
is derived in a similar fashion.
In this section we give some C program fragments to illustrate algorithms for computation of the 3D viewing transformation which transforms world coordinates to eye coordinates.
typedef double Xform3d[4][4];
typedef struct Point3d /* the 3D homogeneous point */
{
double x, y, z, w;
} Point3d, *Point3dPtr, **Point3dHdl;
typedef struct Graph3dView /* the 3D graphics viewing parameters */
{
CWindowPtr wPtr; /* the color graph port */
GrafPtr oldPort; /* the previous graph pointer */
Point3d vrp; /* the view reference point */
Point3d vpn; /* the view plane normal */
Point3d vup; /* the view up direction */
Point3d cop; /* the center of projection (viewpoint) */
Rect viewport; /* the intersection of the viewing pyramid */
double back; /* the z coordinate of the back clipping plane */
double front; /* the z coordinate of the front clipping plane */
double distance; /* the distance of the cop from the view plane */
Xform3d xform; /* the current transformation */
} Graph3dView, *Graph3dViewPtr, **Graph3dViewHdl;
/* ______________________________________________________________
scale3d
This function returns the 3D scaling matrix given
x, y and z scaling factors.
*/
void scale3d(double sx, double sy, double sz, Xform3d scaleMatrix)
{
scaleMatrix[0][0] = sx;
scaleMatrix[0][1] = 0.0;
scaleMatrix[0][2] = 0.0;
scaleMatrix[0][3] = 0.0;
scaleMatrix[1][0] = 0.0;
scaleMatrix[1][1] = sy;
scaleMatrix[1][2] = 0.0;
scaleMatrix[1][3] = 0.0;
scaleMatrix[2][0] = 0.0;
scaleMatrix[2][1] = 0.0;
scaleMatrix[2][2] = sz;
scaleMatrix[2][3] = 0.0;
scaleMatrix[3][0] = 0.0;
scaleMatrix[3][1] = 0.0;
scaleMatrix[3][2] = 0.0;
scaleMatrix[3][3] = 1.0;
} /* End of scale3d */
/* ______________________________________________________________
translate3d
This function returns the 3d translation matrix given
x, y and z translation factors.
*/
void translate3d(double tx, double ty, double tz, Xform3d transMatrix)
{
transMatrix[0][0] = 1.0;
transMatrix[0][1] = 0.0;
transMatrix[0][2] = 0.0;
transMatrix[0][3] = 0.0;
transMatrix[1][0] = 0.0;
transMatrix[1][1] = 1.0;
transMatrix[1][2] = 0.0;
transMatrix[1][3] = 0.0;
transMatrix[2][0] = 0.0;
transMatrix[2][1] = 0.0;
transMatrix[2][2] = 1.0;
transMatrix[2][3] = 0.0;
transMatrix[3][0] = tx;
transMatrix[3][1] = ty;
transMatrix[3][2] = tz;
transMatrix[3][3] = 1.0;
} /* End of translate3d */
/* ______________________________________________________________
identity3d
This function returns the 4 by 4
identity matrix.
*/
void identity3d(Xform3d identity)
{
identity[0][0] = 1.0;
identity[0][1] = 0.0;
identity[0][2] = 0.0;
identity[0][3] = 0.0;
identity[1][0] = 0.0;
identity[1][1] = 1.0;
identity[1][2] = 0.0;
identity[1][3] = 0.0;
identity[2][0] = 0.0;
identity[2][1] = 0.0;
identity[2][2] = 1.0;
identity[2][3] = 0.0;
identity[3][0] = 0.0;
identity[3][1] = 0.0;
identity[3][2] = 0.0;
identity[3][3] = 1.0;
} /* End of identity3d */
/* ______________________________________________________________
rotateX3d
This function returns the x axis rotation matrix given
an angle in radians.
*/
void rotateX3d(double theta, Xform3d rotateMatrix)
{
double sine = sin(theta),
cosine = cos(theta);
rotateMatrix[0][0] = 1.0;
rotateMatrix[0][1] = 0.0;
rotateMatrix[0][2] = 0.0;
rotateMatrix[0][3] = 0.0;
rotateMatrix[1][0] = 0.0;
rotateMatrix[1][1] = cosine;
rotateMatrix[1][2] = sine;
rotateMatrix[1][3] = 0.0;
rotateMatrix[2][0] = 0.0;
rotateMatrix[2][1] = -sine;
rotateMatrix[2][2] = cosine;
rotateMatrix[2][3] = 0.0;
rotateMatrix[3][0] = 0.0;
rotateMatrix[3][1] = 0.0;
rotateMatrix[3][2] = 0.0;
rotateMatrix[3][3] = 1.0;
} /* End of rotateX3d */
/* ______________________________________________________________
rotateY3d
This function returns the y axis rotation matrix given
an angle in radians.
*/
void rotateY3d(double theta, Xform3d rotateMatrix)
{
double sine = sin(theta),
cosine = cos(theta);
rotateMatrix[0][0] = cosine;
rotateMatrix[0][1] = 0.0;
rotateMatrix[0][2] = sine;
rotateMatrix[0][3] = 0.0;
rotateMatrix[1][0] = 0.0;
rotateMatrix[1][1] = 1.0;
rotateMatrix[1][2] = 0.0;
rotateMatrix[1][3] = 0.0;
rotateMatrix[2][0] = -sine;
rotateMatrix[2][1] = 0.0;
rotateMatrix[2][2] = cosine;
rotateMatrix[2][3] = 0.0;
rotateMatrix[3][0] = 0.0;
rotateMatrix[3][1] = 0.0;
rotateMatrix[3][2] = 0.0;
rotateMatrix[3][3] = 1.0;
} /* End of rotateY3d */
/* ______________________________________________________________
rotateZ3d
This function returns the z axis rotation matrix given
an angle in radians.
*/
void rotateZ3d(double theta, Xform3d rotateMatrix)
{
double sine = sin(theta),
cosine = cos(theta);
rotateMatrix[0][0] = cosine;
rotateMatrix[0][1] = sine;
rotateMatrix[0][2] = 0.0;
rotateMatrix[0][3] = 0.0;
rotateMatrix[1][0] = -sine;
rotateMatrix[1][1] = cosine;
rotateMatrix[1][2] = 0.0;
rotateMatrix[1][3] = 0.0;
rotateMatrix[2][0] = 0.0;
rotateMatrix[2][1] = 0.0;
rotateMatrix[2][2] = 1.0;
rotateMatrix[2][3] = 0.0;
rotateMatrix[3][0] = 0.0;
rotateMatrix[3][1] = 0.0;
rotateMatrix[3][2] = 0.0;
rotateMatrix[3][3] = 1.0;
} /* End of rotateZ3d */
/* ______________________________________________________________
shearZ3d
This function produces the Z shearing transformation
which maps an arbitrary line through the origin
and passing through the non-zero point (x, y, z)
into the Z axis without changing the z values of
points on the line.
*/
void shearZ3d(double x, double y, double z, Xform3d zshear)
{
zshear[0][0] = 1.0;
zshear[0][1] = 0.0;
zshear[0][2] = 0.0;
zshear[0][3] = 0.0;
zshear[1][0] = 0.0;
zshear[1][1] = 1.0;
zshear[1][2] = 0.0;
zshear[1][3] = 0.0;
zshear[2][0] = -x / z;
zshear[2][1] = -y / z;
zshear[2][2] = 1.0;
zshear[2][3] = 0.0;
zshear[3][0] = 0.0;
zshear[3][1] = 0.0;
zshear[3][2] = 0.0;
zshear[3][3] = 1.0;
} /* End of shearZ3d */
/* ______________________________________________________________
copy3dXform
This function copies the src 4 by 4 transformation
matrix to the dst 4 by 4 matrix. It is assumed that
the storage for the matrices is allocated in the
calling routine.
*/
void copy3dXform(Xform3d dst, Xform3d src)
{
register int i, j;
for(i = 0; i < 4; i++)
for(j = 0; j < 4; j++)
dst[i][j] = src[i][j];
} /* End of copy3dXform */
/* ______________________________________________________________
mult3dXform
This function multiplies two 4 by 4 transformation
matricies producing a resulting 4 by 4
transformation. For efficiency, we assume that
the last column of the Xform3d is 0 0 0 1
(36 multiplications and 27 additions)
*/
void mult3dXform(Xform3d xform1, Xform3d xform2, Xform3d resultxform)
{
Xform3d result;
/* row 0 (9 * and 6 +) */
result[0][0] = xform1[0][0] * xform2[0][0] +
xform1[0][1] * xform2[1][0] +
xform1[0][2] * xform2[2][0];
result[0][1] = xform1[0][0] * xform2[0][1] +
xform1[0][1] * xform2[1][1] +
xform1[0][2] * xform2[2][1];
result[0][2] = xform1[0][0] * xform2[0][2] +
xform1[0][1] * xform2[1][2] +
xform1[0][2] * xform2[2][2];
result[0][3] = 0.0;
/* row 1 (9 * and 6 +) */
result[1][0] = xform1[1][0] * xform2[0][0] +
xform1[1][1] * xform2[1][0] +
xform1[1][2] * xform2[2][0];
result[1][1] = xform1[1][0] * xform2[0][1] +
xform1[1][1] * xform2[1][1] +
xform1[1][2] * xform2[2][1];
result[1][2] = xform1[1][0] * xform2[0][2] +
xform1[1][1] * xform2[1][2] +
xform1[1][2] * xform2[2][2];
result[1][3] = 0.0;
/* row 2 (9 * and 6 +) */
result[2][0] = xform1[2][0] * xform2[0][0] +
xform1[2][1] * xform2[1][0] +
xform1[2][2] * xform2[2][0];
result[2][1] = xform1[2][0] * xform2[0][1] +
xform1[2][1] * xform2[1][1] +
xform1[2][2] * xform2[2][1];
result[2][2] = xform1[2][0] * xform2[0][2] +
xform1[2][1] * xform2[1][2] +
xform1[2][2] * xform2[2][2];
result[2][3] = 0.0;
/* row 3 ( 9 * and 9 +) */
result[3][0] = xform1[3][0] * xform2[0][0] +
xform1[3][1] * xform2[1][0] +
xform1[3][2] * xform2[2][0] +
xform2[3][0];
result[3][1] = xform1[3][0] * xform2[0][1] +
xform1[3][1] * xform2[1][1] +
xform1[3][2] * xform2[2][1] +
xform2[3][1];
result[3][2] = xform1[3][0] * xform2[0][2] +
xform1[3][1] * xform2[1][2] +
xform1[3][2] * xform2[2][2] +
xform2[3][2];
result[3][3] = 1.0;
/* copy the result */
copy3dXform(resultxform, result);
} /* End of mult3dXform */
/* ______________________________________________________________
transform3dObject
This function multiplies an n array
of Point3d by a 4 by 4
transformation matrix producing
a resulting n array of Point3d.
We assume that the last column of
xform is 0 0 0 1.
( 9n multiplications and 9n additions)
*/
void transform3dObject(int n, Point3d object[], Xform3d xform, Point3d result[])
{
register int i;
for(i = 0; i < n; i++) /* each row */
{
/* column 0 (3 * and 3 +) */
result[i].x = object[i].x * xform[0][0] +
object[i].y * xform[1][0] +
object[i].z * xform[2][0] + xform[3][0];
/* column 1 (3 * and 3 +) */
result[i].y = object[i].x * xform[0][1] +
object[i].y * xform[1][1] +
object[i].z * xform[2][1] + xform[3][1];
/* column 2 (3 * and 3 +) */
result[i].z = object[i].x * xform[0][2] +
object[i].y * xform[1][2] +
object[i].z * xform[2][2] + xform[3][2];
/* column 3 */
result[i].w = object[i].w;
}
} /* End of transform3dObject */
/* ______________________________________________________________
copy3dObject
This function copies a src n array
of Point3d to a dst n array of Point3d.
It is assumed that storage for the src
and dst arrays is allocated in the calling
function.
*/
void copy3dObject(int n, Point3d dst[], Point3d src[])
{
register int i;
for(i = 0; i < n; i++) /* each row */
dst[i] = src[i];
} /* End of copy3dObject */
/* ______________________________________________________________
pitch
This function multiplies the transform associated with
the given graph3dView by an X axis rotation and stores
the resulting transformation as the new graph3dView xform.
*/
void pitch(double theta, Graph3dViewPtr viewPtr)
{
Xform3d rotX;
rotateX3d(theta, rotX);
mult3dXform((*viewPtr).xform, rotX, (*viewPtr).xform);
} /* End of pitch */
/* ______________________________________________________________
roll
This function multiplies the transform associated with
the given graph3dView by an Z axis rotation and stores
the resulting transformation as the new graph3dView xform.
*/
void roll(double theta, Graph3dViewPtr viewPtr)
{
Xform3d rotZ;
rotateZ3d(theta, rotZ);
mult3dXform((*viewPtr).xform, rotZ, (*viewPtr).xform);
} /* End of roll */
/* ______________________________________________________________
yaw
This function multiplies the transform associated with
the given graph3dView by an Y axis rotation and stores
the resulting transformation as the new graph3dView xform.
*/
void yaw(double theta, Graph3dViewPtr viewPtr)
{
Xform3d rotY;
rotateY3d(theta, rotY);
mult3dXform((*viewPtr).xform, rotY, (*viewPtr).xform);
} /* End of yaw */
a/* ______________________________________________________________
dotProduct
This function computes the dot product
(inner product) of two Point3d's. The w
component of the homogeneous representation
of the 3d points is ignored in this
calculation
*/
double dotProduct(Point3dPtr p1, Point3dPtr p2)
{
return (*p1).x * (*p2).x + (*p1).y * (*p2).y + (*p1).z * (*p2).z;
} /* End of dotProduct */
/* ______________________________________________________________
scalarProduct
This function computes the scalar product
of a double and a Point3d. The w component of the
homogeneous representation of the 3d points
is ignored in this calculation.
*/
void scalarProduct(double a, Point3dPtr p, Point3dPtr result)
{
(*result).x = a * (*p).x;
(*result).y = a * (*p).y;
(*result).z = a * (*p).z;
} /* End of scalarProduct */
/* ______________________________________________________________
crossProduct
This function computes the cross product
of two Point3d's. The w component of the
homogeneous representation of the 3d points
is ignored in this calculation.
*/
void crossProduct(Point3dPtr p1, Point3dPtr p2, Point3dPtr result)
{
(*result).x = (*p1).y * (*p2).z - (*p1).z * (*p2).y;
(*result).y = (*p1).z * (*p2).x - (*p1).x * (*p2).z;
(*result).z = (*p1).x * (*p2).y - (*p1).y * (*p2).x;
} /* End of crossProduct */
/* ______________________________________________________________
normalize
This function normalizes the Point3d, a pointer
to which is passed as an argument. The w component of the
homogeneous representation of the 3d point
is ignored in this calculation.
*/
void normalize(Point3dPtr p)
{
double length = sqrt(dotProduct(p, p));
if(length != 0.0)
{
(*p).x /= length;
(*p).y /= length;
(*p).z /= length;
}
} /* End of normalize */
/* ______________________________________________________________
transform3dPoint
This function applies an Xform3d to a
Point3d, transforming that Point3d.
A pointer to a Point3d is passed. The w
component of the homogeneous representation
of the 3d point is ignored in this calculation.
*/
void transform3dPoint(Point3dPtr p, Xform3d xform)
{
Point3d t = *p;
(*p).x = t.x * xform[0][0] +
t.y * xform[1][0] +
t.z * xform[2][0] + xform[3][0];
(*p).y = t.x * xform[0][1] +
t.y * xform[1][1] +
t.z * xform[2][1] + xform[3][1];
(*p).z = t.x * xform[0][2] +
t.y * xform[1][2] +
t.z * xform[2][2] + xform[3][2];
} /* End of transform3dPoint */
/* ______________________________________________________________
subtract3dPoint
This function subtracts Point3dPtr p2 from
Point3dPtr p1 producing Point3dPtr result.
The w component of the homogeneous
representation of the 3d point
is ignored in this calculation.
*/
void subtract3dPoint(Point3dPtr p1, Point3dPtr p2, Point3dPtr result)
{
(*result).x = (*p1).x - (*p2).x;
(*result).y = (*p1).y - (*p2).y;
(*result).z = (*p1).z - (*p2).z;
} /* End of subtract3dPoint */
/* ______________________________________________________________
add3dPoint
This function adds Point3dPtr p2 to
Point3dPtr p1 producing Point3dPtr result.
The w component of the homogeneous
representation of the 3d point
is ignored in this calculation.
*/
void add3dPoint(Point3dPtr p1, Point3dPtr p2, Point3dPtr result)
{
(*result).x = (*p1).x + (*p2).x;
(*result).y = (*p1).y + (*p2).y;
(*result).z = (*p1).z + (*p2).z;
} /* End of add3dPoint */
/* ______________________________________________________________
initGraph3dView
This function initializes the 3D graphics viewing
structure and makes a full screen drawing window.
The Graph3dView is initialized with some default
viewing parameters. These parameters (except for
the wPtr) may be changed before 3D drawing occurs.
*/
void initGraph3dView(Graph3dViewPtr viewPtr)
{
GDHandle mainDevice = GetMainDevice();
Rect mainRect = (**mainDevice).gdRect;
short width, height;
/* set view reference point to origin */
(*viewPtr).vrp.x = 0.0;
(*viewPtr).vrp.y = 0.0;
(*viewPtr).vrp.z = 0.0;
(*viewPtr).vrp.w = 1.0;
/* set view plane normal to z axis */
(*viewPtr).vpn.x = 0.0;
(*viewPtr).vpn.y = 0.0;
(*viewPtr).vpn.z = 1.0;
(*viewPtr).vpn.w = 1.0;
/* set view up direction to y axis */
(*viewPtr).vup.x = 0.0;
(*viewPtr).vup.y = 1.0;
(*viewPtr).vup.z = 0.0;
(*viewPtr).vup.w = 1.0;
/* set view center of projection (viewpoint) */
(*viewPtr).cop.x = 0.0;
(*viewPtr).cop.y = 0.0;
(*viewPtr).cop.z = 720.0;
(*viewPtr).cop.w = 1.0;
/* set view Rect */
width = (mainRect.right - mainRect.left - 5) / 2;
height = (mainRect.bottom - mainRect.top - 43) / 2;
/* order lower left to upper right */
SetRect(&(*viewPtr).viewport, - width, - height, width, height);
/* set back and front Z clipping plane values */
(*viewPtr).back = 1000.0;
(*viewPtr).front = 0.0;
(*viewPtr).distance = (*viewPtr).cop.z - (*viewPtr).vrp.z;
GetPort(&(*viewPtr).oldPort);
(*viewPtr).wPtr = makeDrawingWindow((char *)"\p3D Graphics View",
mainRect.left + 2,
mainRect.top + 40,
mainRect.right - 3,
mainRect.bottom -3);
/* set the transformation to be identity */
identity3d((*viewPtr).xform);
} /* End of initGraph3dView */
/* ______________________________________________________________
viewing
This function produces the viewing transformation matrix
which transforms an abject from world coordinates to
eye coordinates..
*/
void viewing(Graph3dViewPtr viewPtr, Xform3d *view)
{
Point3d t, v, u;
Xform3d tr, rot;
/* project vup on the viewing plane getting the v axis for viewing plane*/
scalarProduct(dotProduct(&((*viewPtr).vpn), &((*viewPtr).vup)), &((*viewPtr).vpn), &t);
subtract3dPoint(&((*viewPtr).vup), &t, &v);
/* compute the u axis of the viewing plane */
crossProduct(&((*viewPtr).vpn), &v, &u);
/* translate the cop + vrp to the origin */
add3dPoint(&((*viewPtr).cop), &((*viewPtr).vrp), &t);
translate3d(-t.x, -t.y, -t.z, tr);
/* compute the rotation matrix */
identity3d(rot);
rot[0][0] = u.x; rot[1][0] = u.y; rot[2][0] = u.z;
rot[0][1] = v.x; rot[1][1] = v.y; rot[2][1] = v.z;
rot[0][2] = (*viewPtr).vpn.x; rot[1][2] = (*viewPtr).vpn.y; rot[2][2] = (*viewPtr).vpn.z;
/* multiply the translation and rotation producing the view transformation */
mult3dXform(tr, rot, *view);
} /* End of viewing */