![\includegraphics[width=5in]{vocab1.aw.eps}](img1.png)
|
John E. Howland
Department of Computer Science
Trinity University
715 Stadium Drive
San Antonio, Texas 78212-7200
Voice: (210) 999-7364
Fax: (210) 999-7477
E-mail: jhowland@Ariel.CS.Trinity.Edu
Web: http://WWW.CS.Trinity.Edu/~jhowland/
Subject Areas: Functional Programming, J Programming Language.
Keywords: Functional Programming, J Programming Lanugage.
A computer is a mechanism for interpreting a language. Computers interpret (perform the actions specified in) sentences in a language which is known as the computer's machine language. It follows, therefore, that a study of the organization of computers is related to the study of the organization of computer languages.
Computer languages are classified in a variety of ways. Machine languages are rather directly interpreted by computers. Higher level computer languages are often somewhat independent from a particular computer and require translation (compilation) to machine language before programs may be interpreted (executed). Languages are also classified as being imperative or applicative depending on the underlying model of computation used by the system.
Abstraction is an important concept in computing. Generally, higher level languages are more abstract. A key tool of abstraction is the use of names. An item of some complexity is given a name. This name is then used as a building block of another item which in turn is named and so on. Abstraction is an important tool for managing complexity of computer programs.
Functional programming is more than just using a functional programming language. The methodology of functional programming is different from that of imperative programming in substantive ways. The functional programming paradigm involves means for reliably deriving programs, analysis of programs, and proofs of program correctness. Because functional programming languages are based on ideas from mathematics, the tools of mathematics may be applied for program derivation, analysis, and proof.
Functional programming languages (applicative languages) differ from conventional programming languages (imperative languages) in at least the following ways:
In applicative languages, names are associated with items which are stored in memory. Once created, in memory, an item is never changed. Names are assigned to items which are stored in memory only if an item needs to be referenced at a later point in time. Items stored in memory are used as arguments for subsequent function applications during the course of a functional computation.
For example, in C (an imperative language) we might write:
int foo; ... foo = 4;
In this example we associate the name foo with a particular memory
cell of size sufficient to hold an integer. Its state at that moment
is unspecified. Later foo is assigned the value 4, i.e., its state
is changed to 4.
In J (an applicative language) we might write:
foo =: 4
An item 4 is created in memory and the name foo is assigned to that item.
Note that in C we say that the value 4 is assigned to foo,
but in J we say that the name foo is assigned to the
value 4. The difference is subtle. With imperative languages the focus is on
the memory cells and how their state changes during the execution of a
program.
With functional languages the focus is on the items in memory. Once an item is created, it is never changed. Names are more abstract in the sense that they provide a reference to something which is stored in memory, but is not necessarily an ordinary data value. Functions are applied to items producing result items and the process is repeated until the computation is complete.
For example, consider the following C (an imperative language) program:
#include <stdio.h>
#include <stdlib.h>
int main (int argc, char *argv[])
{ int sum, count, n;
count = 0;
sum = 0;
while (1 == scanf("%d\n", &n))
{ sum = sum + n;
count++;
}
printf("%f\n", (float)sum / (float)count);
exit(0);
}
This program reads a standard input stream of integer values and
computes the average of these values and writes that average value
on the standard output stream. At the beginning of the average computation,
memory cells count and sum are initialized to have
a state of 0. The memory cell n is changed to each
integer read. Also, the state of sum accumulates the sum
of each of the integers read and the state of count is incremented
to count the number of integers read. Once all of the integers have
be read, their sum is acumulated and the count is known so that the
average may be computed.
To use the C average program one must compile the program.
[jhowland@Ariel jhowland]$ make ave cc ave.c -o ave [jhowland@Ariel jhowland]$ echo "1 2 3" | ave 2.000000 [jhowland@Ariel jhowland]$
In functional languages, computations involve function application. Complex computations require the results of one application be used as the argument for another application. This process is known as functional composition. Functional languages have special compositon rules which may be used in programs. Functional languages, being based on the mathematical idea of a function, benefit from their mathematical heritage. The techniques and tools of mathematics may be used to reason (derive, simplify, transform and prove correctness) about programs.
For example, consider the following J (an applicative language) program:
+/ % #
This program computes the average of a list of numbers in the standard input stream. The result (because no name is assigned to the resulting value) is displayed on the standard output stream.
The J average program has several interesting features.
To use the J average program you put the program and list of numbers in the standard input stream of a J machine (interpreter).
[jhowland@Ariel jhowland]$ echo "(+/ % #) 1 2 3" | jconsole (+/ % #) 1 2 3 2 [jhowland@Ariel jhowland]$
The J average program consists of three functions.
+/ sum
% divide
# tally
When a three function program is applied to a single argument, y, the
following composition rule, fork, is used.
(f g h) y = (f y) g (h y)
In the J average program, f is the function +/, sum, and g
is the function %, divide, and # is the function tally which
counts the number of elements in a list.
More explaination is needed for the J average program.
/ (insert) is a function whose domain is the set
of all available two argument functions (dyads) and whose result
is a function which repeatedly applies its argument function between the items
of the derived function's argument. For example,
+/ produces a function which sums the items
in its argument while */ derives a function which
computes the product of the items in its argument. Most functional languages
allow functions
to be applied to functions producing functions as results. Most imperative
languages do not have this capability.
For example, the derived function +/ sums the items in its argument while
the derived function */ computes the product of the items to which it
is applied.
Imperative languages use language constructs (such as assignment) which describe
the state changes of named memory cells during a computation, for example,
a while loop in C. Such languages have many sentences which produce
no values or which produce changes of other items as a side-effect.
count++; which references
the value of count (the C average program did not use this reference)
and then increments its value by 1 after the reference. The C average
program relied on the side-effect.
Pure functional languages have no side-effects.
Functional programming is important for the following reasons.
Functional languages allow programming without assignments. Structured imperative languages (no goto statements) provide programs which are easier derive, understand, and reason about. Similarly, assignment-free functional languages are easier to derive, understand, and reason about.
Functional languages encourage thinking at higher levels of abstraction. For example, Functions may be applied to functions producing functions as results. Functions are manipulated with the same ease as data. Existing functions may be modified and combined to form new functions. Functional programming involves working in units which are larger than individual statements. Algorithms may be represented without reference to data.
Functional programming languages allow the application of functions to data in agregate rather than being forced to deal with data on an item by item basis. Such applications are free of assignments and independent of evaluation order and provide a mechanism to operate on entire data structures which is an ideal paradigm for parallel computing.
Functional languages have been applied extensively in the field of artificial intelligence. AI researchers have provided much of the early development work on the LISP programming language, which though not a pure functional language, none the less has influenced the design of most functional languages.
Functions languages are often used to develop protoptype implementations and executable specifications for complex system designs. The simple semantics and rigorous mathematical foundations of functional languages make them ideal vehicles for specification of the behavior of complex programs.
Functional programming, because of its mathematical basis, provides a connection to computer science theory. The questions of decidability may be represented in a simpler framework using functional approaches. For example, the essence of denotational semantics involves the translation of imperative programs into equivalent functional programs.
The J programming language [Burk 2001,Bur 2001,Hui 2001] is, a
functional language.
J uses infix notation with primitive functions denoted by
a special symbol, such as + or %, or a special symbol or word followed by the suffix of .
or : .
Each function name may be used as a monad (one argument, written to the right) or as a dyad (two
arguments, one on the left, the other on the right).
The J vocabulary of primitive (built-in) functions is shown in Figures 1 and 2. These
figures show the monadic definition of a function on the left of the * and the dyadic
definition on the right. For example, the function symbol +: represents the monad double and the
dyad not-or (nor).
J uses a simple rule to determine the order of evaluation of functions in expressions.
The argument of a monad or the right argument of a dyad is the value of the entire expression
on the right. The value of the left argument of a dyad is the first item written
to the left of the dyad. Parentheses are used in a conventional manner as punctuation
which alters the order of evaluation. For example, the expression 3*4+5 produces
the value 27, whereas (3*4)+5 produces the value 17.
The evaluation of higher level functions (function producing functions) must be done (of course)
before any functions are applied. Two types of higher level functions exist; adverbs (higher level
monads) and conjunctions (higher level dyads). Figures 1 and 2
show adverbs in bold italic face and conjunctions in bold face. For example, the conjunction
bond (Curry) binds an argument of a dyad to a fixed value producing a monad function as a result
(4&* produces a monad which multiplies by 4).
J is a functional programming language which uses functional composition to model computational
processes. J supports a form of programming known as tacit. Tacit programs have
no reference to their arguments and often use special composition rules known as hooks
and forks. Explicit programs with traditional control structures may also be written.
Inside an explicit definition, the left argument of a dyad is always named x. and the
argument of a monad (as well as the right argument of a dyad) is always named y. .
J supports a powerful set of primitive data structures for lists and arrays. Data (recall that functions have first-class status in J), once created from notation for constants or function application, is never altered. Data items possess several attributes such as type (numeric or character, exact or inexact, etc.) shape (a list of the sizes of each of its axes) and rank (the number of axes). Names are an abstraction tool (not memory cells) which are assigned (or re-assigned) to data or functions.
In functional programming the underlying model of computation is functional composition. A program consists of a sequence of function applications which compute the final result of the program. The J programming language contains a rich set of primitive functions together with higher level functions and composition rules which may be used in programs. To better understand the composition rules and higher level functions we can construct a set of definitions which show some of the characteristics of the language in symbolic form using standard mathematical notation. We start with argument name assignments using character data.
x =: 'x' y =: 'y'
We wish to have several functions named f. g, h, and
i, each of the form:
f =: 3 : 0
'f(',y.,')'
:
'f(',x.,',',y.,')'
)
Rather than enter each of these definitions (and their inverses) we use a function generating definition which uses a pattern.
math_pat =: 3 : 0
'''',y.,'('',y.,'')''',LF,':',LF,'''',y.,'('',x.,'','',y.,'')'''
)
Applying math_pat produces the definition:
math_pat 'f'
'f(',y.,')'
:
'f(',x.,',',y.,')'
Using explicit definition (:) and obverse (:.) we have:
f =: (3 : (math_pat 'f')) :. (3 : (math_pat 'f_inv')) g =: (3 : (math_pat 'g')) :. (3 : (math_pat 'g_inv')) h =: (3 : (math_pat 'h')) :. (3 : (math_pat 'h_inv')) i =: (3 : (math_pat 'i')) :. (3 : (math_pat 'i_inv'))
which produces definitions for each of the functions f. g, h, and
i and a symbolic definition for each inverse function.
Next, we use these definitions to explore some of J's composition rules and higher level functions.
f g y f(g(y)) (f g) y f(y,g(y)) x f g y f(x,g(y)) x (f g) y f(x,g(y)) f g h y f(g(h(y))) (f g h) y g(f(y),h(y)) x f g h y f(x,g(h(y))) x (f g h) y g(f(x,y),h(x,y)) f g h i y f(g(h(i(y)))) (f g h i) y f(y,h(g(y),i(y))) x f g h i y f(x,g(h(i(y)))) x (f g h i) y f(x,h(g(y),i(y))) f@g y f(g(y)) x f@g y f(g(x,y)) f&g y f(g(y)) x f&g y f(g(x),g(y)) f&.g y g_inv(f(g(y))) (h &. (f&g))y g_inv(f_inv(h(f(g(y))))) x f&.g y g_inv(f(g(x),g(y))) f&:g y f(g(y)) x f&:g y f(g(x),g(y)) (f&g) 'ab' f(g(ab)) (f&(g"0)) 'ab' f(g(a)) f(g(b)) (f&:(g"0)) 'ab' f( g(a) g(b) )))) f^:3 y f(f(f(y))) f^:_2 y f_inv(f_inv(y)) f^:0 y y f 'abcd' f(abcd) f/ 2 3$'abcdef' f(abc,def) (f/"0) 2 3$'abcdef' abc def (f/"1) 2 3$'abcdef' f(a,f(b,c)) f(d,f(e,f)) (f/"2) 2 3$'abcdef' f(abc,def) 'abc' f/ 'de' f(abc,de) 'abc' (f"0)/ 'de' f(a,d) f(a,e) f(b,d) f(b,e) f(c,d) f(c,e) 'abc' (f"1)/ 'de' f(abc,de)
Inexact (floating point) numbers are written as 3e10 and can be
converted to exact representations by the verb x:.
x: 3e10 30000000000
Exact rational representations are given by using r to separate
the numerator and denominator.
]a =: 1r2
1r2
(%a)+a^2
9r4
%2
0.5
% x: 2
1r2
Using the reshape verb ($) we create a ![]() table using
exact values.
table using
exact values.
] matrix =: x: 3 3 $ _1 2 5 _8 0 1 _4 3 3 _1 2 5 _8 0 1 _4 3 3 ]inv_matrix =: %. matrix 3r77 _9r77 _2r77 _20r77 _17r77 39r77 24r77 5r77 _16r77 matrix +/ . * inv_matrix 1 0 0 0 1 0 0 0 1
Exact computation of the factorial function (!) produces large numbers.
! x: i. 20 1 1 2 6 24 120 720 5040 40320 362880 3628800 39916800 479001600 6227020800 87178291200 1307674368000 20922789888000 355687428096000 6402373705728000 121645100408832000 ! 100x 93326215443944152681699238856266700490715968264381621468592963895217 59999322991560894146397615651828625369792082722375825118521091686400 0000000000000000000000
To answer the question of how many zeros there are at the end of
!n, we use the function q: which computes the prime
factors of its integer argument. Each zero at the end of !n has a factor
of 2 and 5. It is easy to reason that there are more factors of 2
in !n than factors of 5. Hence the number of zeros at the
end of !n is the number of factors of 5. We can count the
zeros at the end of !n with the following program.
+/ , 5 = q: >: i. 4
0
!6
720
+/ , 5 = q: >: i. 6
1
!20x
2432902008176640000
+/ , 5 = q: >: i. 20
4
J supports complex numbers, using a j to separate real and imaginary parts.
0j1 * 0j1 _1 +. 0j1 * 0j1 NB. real and imaginary parts _1 0 + 3j4 NB. conjugate 3j_4
Other numeric representations include:
1p1 NB. pi
3.14159
2p3 NB. 2*pi^3
62.0126
1x1 NB. e
2.71828
x: 1x1 NB. e as a rational (inexact)
6157974361033r2265392166685
x: 1x_1 NB. reciprocal of e as a rational (inexact)
659546860739r1792834246565
2b101 NB. base 2 representation
5
1ad90 NB. polar representation
0j1
*. 0j1 NB. magnitude and angle
1 1.5708
180p_1 * 1{ *. 3ad30 * 4ad15 NB. angle (in degrees) of product
45
We could define functions rotate and rad2deg as:
rotate =: 1ad1 & *
rad2deg =: (180p_1 & *) @ (1 & {) @ *.
rotate rotates 1 degree counter-clockwise on the
unit circle while rad2deg gives the angle
(in degrees) of the polar representation of a complex number.
rad2deg (rotate^:3) 0j1 NB. angle of 0j1 after 3 degrees rotation
93
+. (rotate^:3) 0j1 NB. (x,y) coordinates on the unit circle
_0.052336 0.99863
+/ *: +. (rotate^:3) 0j1 NB. distance from origin
1
+. rotate ^: (i. 10) 1j0 NB. points on the unit circle
1 0
0.999848 0.0174524
0.999391 0.0348995
0.99863 0.052336
0.997564 0.0697565
0.996195 0.0871557
0.994522 0.104528
0.992546 0.121869
0.990268 0.139173
0.987688 0.156434
A plot of the unit circle is shown in 3.
'x y'=: |: +. rotate ^: (i. 360) 1j0 plot x;y
Howland [How 1998] used the often studied recursive Fibonacci function to describe recursive and iterative processes. In J, the recursive Fibonacci function is defined as:
fibonacci =. monad define if. y. < 2 do. y. else. (fibonacci y. - 1) + fibonacci y. - 2 end. )
Applying fibonacci to the integers 0 through 10 gives:
fibonacci "0 i.11 0 1 1 2 3 5 8 13 21 34 55
Howland [How 1998] also introduced the idea of a continuation; a monad representing the computation remaining in an expression after evaluating a sub-expression.
Given a compound expression e and a sub-expression f of e, the continuation of f in e is the computation in e, written as a monad, which remains to be done after first evaluating f. When the continuation of f in e is applied to the result of evaluating f, the result is the same as evaluating the expression e. Let c be the continuation of f in e. The expression e may then be written as c f.
Continuations provide a ``factorization'' of expressions into two parts; f which is evaluated first and c which is later applied to the result of f. Continuations are helpful in the analysis of algorithms.
Analysis of the recursive fibonacci definition reveals that each
continuation of fibonacci in fibonacci contains an
application of fibonacci. Hence, since at least one continuation
of a recursive application of fibonacci is not the identity
monad, the execution of fibonacci results in a recursive process.
Define a monad, fib_work, to be the number of times fibonacci
is applied to evaluate fibonacci. fib_work is, itself, a
fibonacci sequence generated by the J definition:
fib_work =. monad define if. y. < 2 do. 1 else. 1 + (fib_work y. - 1) + fib_work y. - 2 end. )
Applying fib_work to the integers 0 through 10 gives:
fib_work "0 i.11 1 1 3 5 9 15 25 41 67 109 177
Consider the experiment of estimating how long it would take to evaluate
fibonacci on a workstation. First evaluate fib_work 100.
Since the definition given above results in a recursive process, it is necessary
to create a definition which results in an iterative process when evaluated.
Consider the following definitions:
fib_work_iter =: monad def 'fib_iter 1 1 , y.'
fib_iter =: monad define
('a' ; 'b' ; 'count') =. y.
if. count = 0
do. b
else. fib_iter (1 + a + b) , a , count - 1
end.
)
Applying fib_work_iter to the integers 0 through 10 gives the same result as
applying fib_work:
fib_work_iter "0 i. 11 1 1 3 5 9 15 25 41 67 109 177
Next, use fib_work_iter to compute fib_work 100 (exactly).
fib_iter 100x 57887932245395525494200
Finally, time (time =: 6!:2) the recursive fibonacci definition on arguments not much larger
than 20 to get an estimate of the number of applications/sec the workstation can perform.
(fib_work_iter ("0) 20 21 22 23) % time'fibonacci ("0) 20 21 22 23'
845.138 1367.49 2212.66 3580.19
Using 3500 applications/sec as an estimate we have:
0 3500 #: 57887932245395525494200x 16539409212970150141 700 0 100 365 24 60 60 #: 16539409212970150141x 5244612256 77 234 16 49 1
which is (approximately) 5244612256 centuries!
An alternate experimental approach to solve this problem is to time the recursive
fibonacci definition and look for patterns in the ratios of successive times.
[ experiment =: (4 10 $'fibonacci ') ,. ": 4 1 $ 20 21 22 23 fibonacci 20 fibonacci 21 fibonacci 22 fibonacci 23 t =: time "1 experiment t 2.75291 4.42869 7.15818 11.5908 (1 }. t) % _1 }. t 1.60873 1.61632 1.61924
Note that the ratios are about the same, implying that the time to evaluate
fibonacci is exponential. As an estimate of the time, perform the
computation:
[ ratio =: (+/ % #) (1 }. t) % _1 }. t 1.61476 0 100 365 24 60 60 rep x: ratio^100 205174677357 86 306 9 14 40
This experimental approach produces a somewhat larger estimate of more than 205174677357 centuries. Students should be cautioned about certain flaws in either experimental design.
Suppose we have the following test scores.
[ scores =: 85 79 63 91 85 69 77 64 78 93 72 66 48 76 81 79 85 79 63 91 85 69 77 64 78 93 72 66 48 76 81 79 /:~scores NB. sort the scores 48 63 64 66 69 72 76 77 78 79 79 81 85 85 91 93
A stem-and-leaf diagram has the unit digits (leaves) of observations on one asix and more significant digits (stems) on the other axis. These may be computed from the scores as:
stem =: 10&* @ <. @ %&10 leaf =: 10&| sl_diagram =: ~.@stem ;"0 stem </. leaf sl_diagram /:~scores +--+-----------+ |40|8 | +--+-----------+ |60|3 4 6 9 | +--+-----------+ |70|2 6 7 8 9 9| +--+-----------+ |80|1 5 5 | +--+-----------+ |90|1 3 | +--+-----------+
A more conventional frequency tabulation is given by the definition
fr =: +/"1 @ (=/). The left argument is a range of frequencies
and the right argument is a list of obversations.
4 5 6 7 8 9 fr <. scores%10 1 0 4 6 3 2
This frequency tabulation may be shown as a bar chart (Figure 4) using the built-in ploting library.
pd 'new' pd 'type bar' pd 'xlabel "40" "50" "60" "70" "80" "90"' pd 4 5 6 7 8 9 fr <. scores%10 pd 'show'
When tossing a coin a large number of times, the ratio of the number of heads to the total number of throws should approach a limit of 0.5. However, the absolute value of the difference between heads and tails may become very large. This can be illustrated with the following experiment, the results of which are shown in Figures 5and 6.
toss =: >: i. n =: 500 NB. 500 coin tosses heads =: +/\?n$2 ratio =: heads % toss diff =: |toss - 2*heads toss =: >: i. n =:10 NB. a small trial toss;ratio +--------------------+------------------------------------------------------------+ |1 2 3 4 5 6 7 8 9 10|1 0.5 0.666667 0.75 0.6 0.666667 0.714286 0.625 0.555556 0.5| +--------------------+------------------------------------------------------------+ toss;diff +--------------------+-------------------+ |1 2 3 4 5 6 7 8 9 10|1 0 1 2 1 2 3 2 1 0| +--------------------+-------------------+
We examine some elementary ideas from number theory to demonstrate the expressive power of J.
12 +. 5 NB. greatest common divisor 1 27 +. 3 3 1 2 3 4 5 6 7 8 9 10 11 12 +. 12 1 2 3 4 1 6 1 4 3 2 1 12 NB. The numbers <: 12 which are coprime with 12 (1 = 1 2 3 4 5 6 7 8 9 10 11 12 +. 12) # 1 2 3 4 5 6 7 8 9 10 11 12 1 5 7 11 NB. The numbers <: 12 which have common factors with 12 (-. 1 = 1 2 3 4 5 6 7 8 9 10 11 12 +. 12) # 1 2 3 4 5 6 7 8 9 10 11 12 2 3 4 6 8 9 10 12 NB. 8 9 19 have common factors but do not divide 12 ((-. 1 = 1 2 3 4 5 6 7 8 9 10 11 12 +. 12) # 1 2 3 4 5 6 7 8 9 10 11 12) | 12 0 0 0 0 4 3 2 0
Next we generalize these expressions as functions totatives
and non_totatives.
totatives =: 3 : 0 p =. >: i. y. (1 = p +. y.) # p ) non_totatives =: 3 : 0 p =. >: i. y. (-. 1 = p +. y.) # p ) totatives 12 1 5 7 11 totatives 28 1 3 5 9 11 13 15 17 19 23 25 27 non_totatives 12 2 3 4 6 8 9 10 12 non_totatives 15 3 5 6 9 10 12 15 divisors =: 3 : 0 p =. non_totatives y. (0 = p | y.) # p ) divisors "0 (12 27 100) 2 3 4 6 12 0 0 0 3 9 27 0 0 0 0 0 2 4 5 10 20 25 50 100
The number of totatives of n is called the totient of n.
We can define totient =: # @ totatives. An alternate
(tacit) definition is phi =: * -.@%@~.&.q:.
(totient "0) 100 12 40 4 phi 100 12 40 4
Euler's theorem states that given an integer ![]() coprime with
coprime with
![]() , then
, then
![]() . This leads to the
definition:
. This leads to the
definition:
euler =: 4 : 'x. (y.&| @ ^) totient y.' 2 euler 19 1 2 euler 35 1 3 euler 28 1 3 euler 205 1 3 euler 200005 1
The product of two totatives of ![]() ,
, ![]() is a totative of n.
We can see this by using J's table (/) adverb.
is a totative of n.
We can see this by using J's table (/) adverb.
totatives 12 1 5 7 11 12 | 1 5 7 11 */ 1 5 7 11 1 5 7 11 5 1 11 7 7 11 1 5 11 7 5 1
We notice that we have a group (closure, identity element, inverses,
and associativity).
There is a table adverb which may be used to present
the above results.
table
1 : 0
u.table~ y.
:
(' ';,.x.),.({.;}.)":y.,x.u./y.
)
12&|@* table totatives 12
+--+-----------+
| | 1 5 7 11|
+--+-----------+
| 1| 1 5 7 11|
| 5| 5 1 11 7|
| 7| 7 11 1 5|
|11|11 7 5 1|
+--+-----------+
Notice that addition residue 12 of the totatives of 12 do not form a group.
12&|@+ table 0 , totatives 12
+--+------------+
| | 0 1 5 7 11|
+--+------------+
| 0| 0 1 5 7 11|
| 1| 1 2 6 8 0|
| 5| 5 6 10 0 4|
| 7| 7 8 0 2 6|
|11|11 0 4 6 10|
+--+------------+
Consider totatives of a prime value.
p: 6 17 totatives 17 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17&|@* table totatives 17 +--+-----------------------------------------------+ | | 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16| +--+-----------------------------------------------+ | 1| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16| | 2| 2 4 6 8 10 12 14 16 1 3 5 7 9 11 13 15| | 3| 3 6 9 12 15 1 4 7 10 13 16 2 5 8 11 14| | 4| 4 8 12 16 3 7 11 15 2 6 10 14 1 5 9 13| | 5| 5 10 15 3 8 13 1 6 11 16 4 9 14 2 7 12| | 6| 6 12 1 7 13 2 8 14 3 9 15 4 10 16 5 11| | 7| 7 14 4 11 1 8 15 5 12 2 9 16 6 13 3 10| | 8| 8 16 7 15 6 14 5 13 4 12 3 11 2 10 1 9| | 9| 9 1 10 2 11 3 12 4 13 5 14 6 15 7 16 8| |10|10 3 13 6 16 9 2 12 5 15 8 1 11 4 14 7| |11|11 5 16 10 4 15 9 3 14 8 2 13 7 1 12 6| |12|12 7 2 14 9 4 16 11 6 1 13 8 3 15 10 5| |13|13 9 5 1 14 10 6 2 15 11 7 3 16 12 8 4| |14|14 11 8 5 2 16 13 10 7 4 1 15 12 9 6 3| |15|15 13 11 9 7 5 3 1 16 14 12 10 8 6 4 2| |16|16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1| +--+-----------------------------------------------+
and
17&|@+ table 0 , totatives 17 +--+--------------------------------------------------+ | | 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16| +--+--------------------------------------------------+ | 0| 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16| | 1| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0| | 2| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1| | 3| 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2| | 4| 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3| | 5| 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4| | 6| 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5| | 7| 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6| | 8| 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7| | 9| 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8| |10|10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9| |11|11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10| |12|12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11| |13|13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12| |14|14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13| |15|15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14| |16|16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15| +--+--------------------------------------------------+
Finally, consider the definition powers which raises
the totatives to the totient power.
powers =: 3 : '(totatives y.) (y.&| @ ^) / i. 1 + totient y.' powers 12 1 1 1 1 1 1 5 1 5 1 1 7 1 7 1 1 11 1 11 1 powers 17 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 4 8 16 15 13 9 1 2 4 8 16 15 13 9 1 1 3 9 10 13 5 15 11 16 14 8 7 4 12 2 6 1 1 4 16 13 1 4 16 13 1 4 16 13 1 4 16 13 1 1 5 8 6 13 14 2 10 16 12 9 11 4 3 15 7 1 1 6 2 12 4 7 8 14 16 11 15 5 13 10 9 3 1 1 7 15 3 4 11 9 12 16 10 2 14 13 6 8 5 1 1 8 13 2 16 9 4 15 1 8 13 2 16 9 4 15 1 1 9 13 15 16 8 4 2 1 9 13 15 16 8 4 2 1 1 10 15 14 4 6 9 5 16 7 2 3 13 11 8 12 1 1 11 2 5 4 10 8 3 16 6 15 12 13 7 9 14 1 1 12 8 11 13 3 2 7 16 5 9 6 4 14 15 10 1 1 13 16 4 1 13 16 4 1 13 16 4 1 13 16 4 1 1 14 9 7 13 12 15 6 16 3 8 10 4 5 2 11 1 1 15 4 9 16 2 13 8 1 15 4 9 16 2 13 8 1 1 16 1 16 1 16 1 16 1 16 1 16 1 16 1 16 1
In this section we discuss the representation of polynomials and
operations defined on polynomials. A polynomial is determined
by its coefficients so we represent the polynomial as
a list of coefficients written in ascending order rather than the usual decending
order. For example, the polynomial ![]() is written
as
is written
as 5 2 0 1.
To evaluate a polynomial we write:
peval =: (#. |.) ~ 5 2 0 1 peval 3 38
A primitive for polynomial evaluation, p. is provided.
5 2 0 1 p. 3 38
To add or subtract two polynomials we add or subtract the coefficients of like terms.
psum =: , @ (+/ @ ,: & ,:) pdif =: , @ (-/ @ ,: & ,:) 1 2 psum 1 3 1 2 5 1 3 psum 1 3 1 4 3 1 1 2 pdif 1 3 1 0 _1 _1
Next we consider the product and derivative of polynomials.
If we make a product table, the coefficients of like terms
lie along the oblique diagonals of that table. The oblique
adverb /. allows access to these diagonals.
pprod =: +/ /. @ (*/) 1 2 pprod 1 3 1 1 5 7 2 pderiv =: 1: }. ] * i. @ # pderiv 1 3 3 1 3 6 3 p.. 1 3 3 1 NB. There is a primitive for derivative 3 6 3
To illustrate the ease with which higher level functional abstractions may be expressed, consider the problem of working with matrices whose elements are polynomials. We represent these as a boxed table. For example,
[ m =: 2 2 $ 1 2 ; 1 2 1 ; 1 3 3 1 ; 1 4 6 4 1 +-------+---------+ |1 2 |1 2 1 | +-------+---------+ |1 3 3 1|1 4 6 4 1| +-------+---------+ [ n =: 2 3 $ 1 2 3 ; 3 2 1 ; 1 0 1 ; 3 3 3 3 ; _1 _2 3; 3 4 5 +-------+-------+-----+ |1 2 3 |3 2 1 |1 0 1| +-------+-------+-----+ |3 3 3 3|_1 _2 3|3 4 5| +-------+-------+-----+
Next, we define new versions of psum, pdif, and pprod
which assume their arguments are boxed polynomials.
psumb =: psum &. > pdifb =: pdif &. > pprodb =: pprod &. >
Then we can define a matrix product for these matrices whose elements are polynomials as:
pmp =: psumb / . pprodb
m pmp n
+---------------------+---------------+------------------+
|4 13 19 18 9 3 |2 4 3 6 3 |4 12 17 16 5 |
+---------------------+---------------+------------------+
|4 20 45 61 56 36 15 3|2 5 5 8 14 11 3|4 19 43 60 52 25 5|
+---------------------+---------------+------------------+
m pmp m
+--------------------+-----------------------+
|2 9 14 10 5 1 |2 10 20 22 15 6 1 |
+--------------------+-----------------------+
|2 12 30 42 37 21 7 1|2 13 38 66 75 57 28 8 1|
+--------------------+-----------------------+
m pmp^:0 m
+-------+---------+
|1 2 |1 2 1 |
+-------+---------+
|1 3 3 1|1 4 6 4 1|
+-------+---------+
m pmp^:1 m
+--------------------+-----------------------+
|2 9 14 10 5 1 |2 10 20 22 15 6 1 |
+--------------------+-----------------------+
|2 12 30 42 37 21 7 1|2 13 38 66 75 57 28 8 1|
+--------------------+-----------------------+
m pmp^:2 m
+----------------------------------------+----------------------------------------------+
|4 29 88 152 176 148 88 36 9 1 |4 31 106 217 304 309 230 123 45 10 1 |
+----------------------------------------+----------------------------------------------+
|4 35 137 323 521 613 539 353 168 55 11 1|4 37 158 418 772 1055 1094 864 513 222 66 12 1|
+----------------------------------------+----------------------------------------------+
m pmp^:10 x: &. > m
+-------------------------------------------------...
|1024 29952 424704 3899184 26124316 136500501 5803...
+-------------------------------------------------...
|1024 31488 471040 4577232 32551980 180983051 8205...
+-------------------------------------------------...
Iverson and others have written several books which use J to describe a number of computing related topics. One of these [Ive 1995] uses J in a rather formal way to express algorithms and proofs of topics covered in [Gra 1989]. Following is an example from the introduction of [Ive 1995].
A theorem is an assertion that one expression l is equivalent to another r. We can express this relationship in J as:
t=: l -: rThis is the same as saying that l must match r, that is, t must be the constant function 1 for all inputs.
t is sometimes called a tautology. For example, suppose
l =: +/ @ i. NB. Sum of integers r =: (] * ] - 1:) % 2:If we define n =: ] , the right identity function, the we can rewrite the last equations as:
r =: (n * n - 1:) % 2:Next,
t =: l -: rNotice that by experimentation, t seems to always be 1 no matter what input argument is used.
t 1 2 3 4 5 6 7 8 9 1 1 1 1 1 1 1 1 1A proof of this theorem is a sequence of equivalent expressions which leads from l to r.
l
+/ @ i. Definition of l
+/ @ |. i. Sum is associative and commutative
(|. is reverse)
((+/ @ i.) + (+/ @ |. @ i.)) % 2: Half sum of equal values
+/ @ (i. + |. @ i.) % 2: Summation distributes over addition
+/ @ (n # n - 1:) % 2: Each term is n -1; there are n terms
(n * n - 1:) % 2: Definition of multiplication
r Definition of r
Of course, each expression in the above proof is a simple program and the proof is
a sequence of justifications which allow transformation of one expression to the next.
Iverson discusses the role of computers in mathematical notation in [Ive 2000]. In this paper he quotes
A. N. Whitehead
By relieving the brain of all unnecessary work, a good notation sets it free to concentrate on more advanced problems, and in effect increases the mental power of the race.F. Cajori
Some symbols, likeA. de Morgan,
,
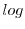
, that were used originally for only positive integral values of
stimulated intellectual experimentation when
is fractional, negative, or complex, which led to vital extensions of ideas.
Mathematical notation, like language, has grown up without much looking to, at the dictates of convenience and with the sanction of the majority.
Other noteworth quotes with relevance for J include:
Friedrich Engels
In science, each new point of view calls forth a revolution in nomenclature.
Bertrand Russell
A good notation has a subtlety and suggestiveness which at times make it almost seem like a live teacher.
A. N. Whitehead, in Introduction to Mathematics
It is a profoundly erroneous truism, repeated by all copy books and by eminent people when they are making speeches, that we should cultivate the habit of thinking of what we are doing. The precise opposite is the case. Civilization advances by extending the number of important operations which we can perform without thinking about them.
Certainly, the J notation, being executable, relieves the brain the task
of doing routine calculations letting it concentrate on the ideas behind
the calculation. The notation also removes certain ambiguities of
mathematical notation, not confusing _3 (minus three) with
the application -3 (negate three).
An example of the kind of extensions provided by a good notation to
which Cajori refers can be found in the notation for outer product
(spelled .).
+/ . * (matrix product) expressed as an outer product led to
other useful outer products such as +./ . *..
Sadly, J is not widely accepted within computer science and even stranger is its lack of acceptance within mathematics.