Computing Fibonacci Numbers¹

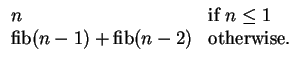
Date: 2000 Jan 11

My coauthors and I are presenting a paper entitled ``Accurate Approximations for Asian Options'' at the Symposium on Discrete Algorithms conference so I will not be with you today. I will return to San Antonio tomorrow afternoon.

Introduction

The sequence of Fibonacci numbers begins 0, 1, 1, 2, 3, 5, 8, 13, 21, .... In general, the Fibonacci numbers can be defined by the rule

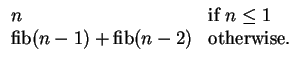
$\ensuremath{\mathop{\rm fib}\nolimits(n)}$ = $\displaystyle \left\{\vphantom{ \begin{array}{ll} n & \text{if } n \leq 1 \\ ... ...emath{\mathop{\rm fib}\nolimits(n-2)} & \text{otherwise.} \end{array} }\right.$ $\displaystyle \begin{array}{ll} n & \text{if } n \leq 1 \\ \ensuremath{\math... ... + \ensuremath{\mathop{\rm fib}\nolimits(n-2)} & \text{otherwise.} \end{array}$ $\displaystyle \left.\vphantom{ \begin{array}{ll} n & \text{if } n \leq 1 \\ ... ...emath{\mathop{\rm fib}\nolimits(n-2)} & \text{otherwise.} \end{array} }\right.$

Today's group project is to implement Fibonacci numbers three different ways. This will demonstrate how different algorithms solving the same problem require different times.

Instructions

1.

Read through the three different approaches to implementing Fibonacci numbers.

2.

Split the class into four different groups:

a group implementing the recursive Fibonacci definition
a (larger) group implementing the Fibonacci numbers using memoization
a group implementing the constant time algorithm for Fibonacci numbers
two people to record the algorithms' running times

3.

Program the various algorithms.

4.

Run the algorithms to compute Fibonacci numbers, recording the running times in a spreadsheet. Try to determine what functions the running times look like.

Recursive Definition of Fibonacci Numbers

The recursive definition appears in the Introduction. Implement it recursively.

Linear Time Implementation

Directly using the recursive definition is wasteful because many Fibonacci numbers are computed repeatedly. For example, when computing $\ensuremath{\mathop{\rm fib}\nolimits(5)}$ , $\ensuremath{\mathop{\rm fib}\nolimits(4)}$ is computed once, $\ensuremath{\mathop{\rm fib}\nolimits(3)}$ is computed twice, $\ensuremath{\mathop{\rm fib}\nolimits(2)}$ is computed three times, and $\ensuremath{\mathop{\rm fib}\nolimits(1)}$ is computed five times. (The number of computations is a Fibonacci sequence in itself!)

We can greatly reduce the running time by storing the result of computing each number. For example, when computing $\ensuremath{\mathop{\rm fib}\nolimits(5)}$ , we must compute $\ensuremath{\mathop{\rm fib}\nolimits(3)}$ . When we do so the first time, we can store its value in the third position of an array. Thus, when computing $\ensuremath{\mathop{\rm fib}\nolimits(n)}$ , we check if it has already been computed. If so, we have the answer. Otherwise, we (recursively) compute the answer, store it, and then return it. This should greatly reduce the running time, but we need an array with potentially infinite size because we do not know a priori how large a Fibonacci number we need to compute.

First, convince yourself that, when computing $\ensuremath{\mathop{\rm fib}\nolimits(n)}$ using this scheme, we will store $\ensuremath{\mathop{\rm fib}\nolimits(0)}$ , $\ensuremath{\mathop{\rm fib}\nolimits(1)}$ , $\ensuremath{\mathop{\rm fib}\nolimits(2)}$ , ..., $\ensuremath{\mathop{\rm fib}\nolimits(n)}$ , in that order.

Second, we note that storing these values in an array will not work because we cannot guarantee the array will be large enough. Instead, we can turn to our friend the Standard Template Library. (For the rest of this section, we will assume the Fibonacci function returns a value of type long double. See below.)

A vector<long double> is an array of long doubles that can grow when needed.

To create a vector:: vector<long double> v
Creates a vector with zero long double elements.
To access the element at index 17:: v[17]
For example, one can assign to this element using v[17] = 4.5. Note the vector must have size at least 18 elements to access v[17].
To append an entry:: v.push_back(3.4)
Enlarges the vector's size by one, placing 3.4 in the newly created (and last) position. Nothing is returned.
To determine a vector's size:: v.size()
Returns the vector's size. This can be different than the number of elements in the vector.

If one uses only push_back, the number of elements in the vector and the vector's size are exactly the same. If one uses the size(n) member function to make the vector have size n, some positions may be unspecified, just as an array's elements are unspecified when it is created.

The vector of Fibonacci numbers could be a global variable, but avoiding global variables is usually a good idea. One approach is to package together the vector and the Fibonacci function in a class. Another approach is to define the Fibonacci function with a static vector (if you know what that means).

When timing this implementation, be sure to start the program with an empty vector to be fair to the other implementations.

A Constant Time Algorithm

Édouard Lucas discovered a formula for the Fibonacci numbers:

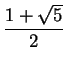
$\ensuremath{\mathop{\rm fib}\nolimits(n)}$ = $\displaystyle {\frac{1}{\sqrt{5}}}$ $\displaystyle \left(\vphantom{ \left(\frac{1 + \sqrt{5}}{2}\right)^n - \left(\frac{1 - \sqrt{5}}{2}\right)^n }\right.$ $\displaystyle \left(\vphantom{\frac{1 + \sqrt{5}}{2}}\right.$ $\displaystyle {\frac{1 + \sqrt{5}}{2}}$ $\displaystyle \left.\vphantom{\frac{1 + \sqrt{5}}{2}}\right)^{n}_{}$ - $\displaystyle \left(\vphantom{\frac{1 - \sqrt{5}}{2}}\right.$ $\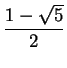displaystyle {\frac{1 - \sqrt{5}}{2}}$ $\displaystyle \left.\vphantom{\frac{1 - \sqrt{5}}{2}}\right)^{n}_{}$ $\displaystyle \left.\vphantom{ \left(\frac{1 + \sqrt{5}}{2}\right)^n - \left(\frac{1 - \sqrt{5}}{2}\right)^n }\right)$ .

The right term is less than one so it goes to zero as n increases. If we incorporate floor functions, the formula becomes even simpler:

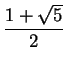
$\ensuremath{\mathop{\rm fib}\nolimits(n)}$ = $\displaystyle \left\lfloor\vphantom{ \frac{1}{\sqrt{5}} \left(\frac{1 + \sqrt{5}}{2}\right)^n + \frac{1}{2}}\right.$ $\displaystyle {\frac{1}{\sqrt{5}}}$ $\displaystyle \left(\vphantom{\frac{1 + \sqrt{5}}{2}}\right.$ $\displaystyle {\frac{1 + \sqrt{5}}{2}}$ $\displaystyle \left.\vphantom{\frac{1 + \sqrt{5}}{2}}\right)^{n}_{}$ + $\displaystyle {\textstyle\frac{1}{2}}$ $\displaystyle \left.\vphantom{ \frac{1}{\sqrt{5}} \left(\frac{1 + \sqrt{5}}{2}\right)^n + \frac{1}{2}}\right\rfloor$ .

The floor function $\lfloor$ x $\rfloor$ yields the smallest integer less than or equal to x. For example, $\lfloor$ 7.4 $\rfloor$ = $\lfloor$ 7 $\rfloor$ = 7.

The Gnu C Library may be useful when implementing this algorithm.

Instructions Pertinent to All Implementations

Assume we wish to compute $\ensuremath{\mathop{\rm fib}\nolimits(n)}$ for nonnegative n only. If you desire, you can use unsigned longs for both the parameter and the return type. Using a return type of doubles or long doubles will extend the domain for which Fibonacci numbers can be computed. This is necessary for the linear and constant time algorithms. For example, the function declaration could be

long double fibonacci(unsigned long n).

To time your code, we add a function to print the running time of your program.

1.: Copy timer.h to the directory containing the rest of your code.
2.: Add #include "timer.h" near the top of your program.
3.: Add timer(cout) near the bottom of your main function. If you want to print the output to an output stream named out, replace cout with out.

For this project, I grant members of CS1321 permission to use the timer code.

The smallest unit of time most computers running Linux is 10 msec so the data may be noisy for small running times. To tell the compiler to produce very optimized code, use the -O3 compiler code. For example,

g++ -O3 foo.cc.

Recording the Running Times

Use your favorite graphing package or Microsoft Excel to produce plots comparing n and the time to compute $\ensuremath{\mathop{\rm fib}\nolimits(n)}$ . Try to find an equation and its R² value for the running times. What does the R² value mean?

I am not a regular Microsoft Excel user, but here are some tips I found useful.

I preferred a scatter X-Y chart.
One can add a trendline to a chart using the Chart/Add Trendline menu option.
Under the trendline options tab is the ability to give the trendline's equation and R² value.

History and an Application of Fibonacci Numbers

Leonardo Fibonacci² (c. 1170-c. 1240) introduced Fibonacci numbers in 1202. Édouard Lucas popularized the term ``Fibonacci numbers.'' These numbers occur so frequently in mathematics that an entire journal named Fibonacci Quarterly exists.

Fibonacci numbers can model the number of pairs of rabbits on an island. Initially, a pair (male and female) of newborn rabbits is placed on an island. Each sexually mature pair of rabbits can breed every month, but newborns must wait two months to become mature. At the beginning (just before the rabbits are placed on the island), there are no pairs of rabbits ( $\ensuremath{\mathop{\rm fib}\nolimits(0)} = 0$ ). At the end of the first and second months, there is still one pair of rabbits ( $\ensuremath{\mathop{\rm fib}\nolimits(1)} = \ensuremath{\mathop{\rm fib}\nolimits(2)} = 1$ ). Then they give birth to a pair of rabbits ( $\ensuremath{\mathop{\rm fib}\nolimits(3)} = 2$ ). The next month, the original pair gives birth to another pair of rabbits, but the second pair is not yet sexually mature ( $\ensuremath{\mathop{\rm fib}\nolimits(4)} = 3$ ). The next month the second pair of rabbits are mature so two pairs of rabbits give birth ( $\ensuremath{\mathop{\rm fib}\nolimits(5)} = 5$ ). The process continues.

Footnotes

... Fibonacci ²: Born in Pisa about 1180, Fibonacci (short for filius Bonacci, or ``son of Bonacci'') was a merchant traveling through the Mideast. He introduced Arabic notation for numerals and algorithms for arithmetic in his book Liber Abaci.

2000-01-06

Computing Fibonacci Numbers1