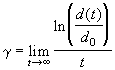 , (1)
, (1)Infinite and Finite Time Lyapunov Exponents
and their use for Measuring the Stability
of Orbits in the Outer Solar System
Mark Lewis
Infinite Time Lyapunov Exponents
When Isaac Newton wrote the Principia, he had something of an itinerary other than simply advancing mankindís understanding of how the universe works. Newton wanted a stable, predictable universe that fit with his views of how God would have created it. While Newtonís predisposition didnít alter the validity of his laws or the complexity they harbored, his influence was great enough that it caused many people to follow him in his use of linearization and perturbation theory to show that under his laws the universe was generally stable and predictable. Many well educated people followed his lead without regard to the fact that such a rule obviously didnít hold in the world of people that surrounded them.
There were definitely signs that pointed in the opposite direction. For example, perturbation theory was completely incapable of accurately predicting the future position of the moon. And along this same line, people were aware of the difficulties associated with the general three body problem. However, even with this knowledge, it was not until 1889 that people became aware that our solar system was not clockwork. That was the year that Oscar II, King of Sweden and Norway, turned sixty (Peterson, 1993). In honor of this event, a contest was proposed by a mathematics professor named Gösta Mittag-Leffler, as was a customary practice at the time. The objective of the contest was to address one of four problems in a brief paper. One of these problems was to show that the solar system was stable or unstable. It was this problem that Jules Henry Poincaré choose to address. The result was a 200 page paper showing that the solar system was unstable which was easily given the highest honors in the contest.
Poincaréís approach to this problem was to see how small changes in the initial conditions propagated over time. He began by looking at periodic orbits then perturbing them slightly to see if they remained in a fixed region of space. He found that they did not. This work is considered by many to be the birth of the area now called chaos. This type of sensitive dependence on initial conditions is at the root of chaos and is quantified by the Lyapunov exponent.
The Lyapunov exponent is defined as the exponential rate at which nearby trajectories diverge. For an n-dimensional system there are n such rates of divergence. To see this, picture a sphere evolving over time through some given set of equations. As the sphere is evolved, it can be stretched in some directions and squeezed in others. Stretching implies a positive Lyapunov exponent while squeezing implies a negative one. In conservative systems the volume of such a sphere is conserved over time which implies that the sum of the Lyapunov exponents is zero. The gravitational systems which are considered later in this paper are Hamiltonian, and therefore conservative. However, for most purposes, and all those of this paper, only the maximum Lyapunov exponent is considered, as over time it is the stretching along the direction of the maximum Lyapunov exponent that determines how sensitive a system is to initial conditions. Generally this is expressed in the limit as time goes to infinity, and can be written numerically as
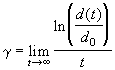 , (1)
, (1)
where d(t) is the separation between the trajectories at time t, and d0 is their separation at time zero.
Equation 1 is deceptively simple and could lead one to believe that the measuring of maximum Lyapunov exponents is a direct and easy process. Unfortunately this is not the case. There are many reasons for this, and as a result of these difficulties special methods must be applied just for measuring the standard infinite time Lyapunov exponent.
One reason that Equation 1 is not directly usable is that when it is of interest, the system under consideration tends to be bounded. In fact, some contend that the Lyapunov exponent is a measure of chaos only in bound systems (Tsonis, 1992). This would imply that their infinite time Lyapunov exponents are zero. A second reason is that the rate of separation of trajectories is different in different regions of the phase space. If the trajectories actually separate too much they will move into different regions, and further separation does not truly indicate the expansion rates around either trajectory.
As a result, any method that is used for measuring the infinite time Lyapunov exponent must either avoid these problems or must somehow keep the trajectories together. The first method I will describe takes the later route. This method is called renormalization, and it is, in principle, a very simple method. A particle is placed on the trajectory of interest, x1(t), while another particle is placed some distance, d0, away at x2(t). The particles are advanced in time until some designated event occurs. At that time, to prevent the second particle from moving too far from the first, it is brought back towards it along the line through the two to their initial separation, d0. Using this method, the value of the Lyapunov exponent after the lth renormalization is
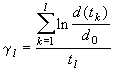 , (2)
, (2)
where d(tk) is the separation between the particles before the kth renormalization (Wisdom, 1983). This value is equal to the true Lyapunov exponent when
![]() . (3)
. (3)
If this is not the case, then the renormalization algorithm will return some other value.
In the description above, the renormalization occurs at some unspecified event. In practice there are two "events" that are used to trigger the renormalization: a specified time interval or distance between the particles. Whichever event is chosen, one must be careful to avoid having renormalizations occur too frequently or too rarely. If they occur too rarely, the secondary particle will simply move too far from the first negating the reasons for using renormalization in the first place. If, on the other hand, they occur too frequently, only the linear characteristics of the expansion are manifest. This results in equation 3 not being true, and hence, the algorithm returns something other than the actual Lyapunov exponent. It turns out that for constant time renormalization to work, the time period for renormalizations must be within a factor of five or so of 1/g . Because g is the quantity we are trying to find, this very nearly amounts to having to know the answer before you can find it. It poses another problem as well; in many cases, it is more efficient to calculate more than one trajectory at a time. If the Lyapunov exponents of these different trajectories vary by any significant amount, then they must either be assigned different renormalization times, or processed in separate runs. The constant distance method doesnít suffer from these limitations and therefore, allows for multiple trajectories to be calculated simultaneously.
Renormalization poses one other difficulty. Assume that instead of being exponential, the divergence rate for a pair of adjacent trajectories is linear, ![]() . In such a situation, the proper Lyapunov exponent is zero. However, by simply plugging this function into equation 2, one can see that this will not happen. For constant time renormalization, the algorithm returns
. In such a situation, the proper Lyapunov exponent is zero. However, by simply plugging this function into equation 2, one can see that this will not happen. For constant time renormalization, the algorithm returns 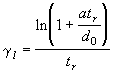 , where tr is the time interval between renormalizations, while the constant distance method returns
, where tr is the time interval between renormalizations, while the constant distance method returns ![]() , where c is the multiple of d0 at which renormalizations are done. Because both algorithms return a non-zero value is it very difficult, using these algorithms, to distinguish between when a trajectory is chaotic and when it is regular.
, where c is the multiple of d0 at which renormalizations are done. Because both algorithms return a non-zero value is it very difficult, using these algorithms, to distinguish between when a trajectory is chaotic and when it is regular.
Another method for measuring infinite time Lyapunov exponents is described by Wisdom (1983). This method does not use a second or shadow particle. Instead, a separate differential equation that models rate of change of the separation of trajectories is integrated at the same time as the equations of motion for the primary particles. To see how this works consider the system described by the equation
![]() . (4)
. (4)
Selecting a trajectory separated from x by some small displacement d we get a second equation describing its motion of the form
![]() . (5)
. (5)
By Taylor expanding the right side of equation 5, and keeping only terms linear in d, then subtracting equation 4 from this produces an equation describing the evolution of d in time,
![]() . (6)
. (6)
Because this equation is linear in d, absolute scale is irrelevant, which is the reason that renormalization procedures are acceptable. The Lyapunov exponent can thus be calculated by integrating equations 4 and 6 simultaneously, then performing an exponential fit to d(t).
A plethora of other methods exist for calculating Lyapunov exponents. Many, such as those described in Geist, et al. (1990) use different matrix decomposition methods to calculate the full spectrum of Lyapunov exponents for a system. As one of the primary focuses of this paper though is finite time or local Lyapunov exponents, at this time I shall go into a discussion of how they are different from their infinite time counterparts, and how they can be measured. Then after introducing the concept we will look at applications of it.
Finite Time/Local Lyapunov Exponents
While infinite time Lyapunov exponents are suitable for characterizing global behaviors of a system, in many situations it is more desirable to have a local measure of the rate at which trajectories diverge. Over a finite time period this can be done by measuring the divergence of adjacent trajectories over some finite period t . This approach was taken by Nese (1989) in which he defines this divergence rate, L, as
![]() . (7)
. (7)
It should probably be noted at this point that Nese actually used a log2 in his paper instead of ln. The use of the base two log is common in information theory, as it gives the rate at which binary digits are "lost", which is of great significance when considering the propagation of round-off errors in numerical computations. I have chosen to use the natural log, primarily to keep some uniformity with the previous section.
With this formula, it is simple to see that the maximum Lyapunov exponent can be rewritten as
![]() . (8)
. (8)
This definition of L(x) as something of a finite time Lyapunov exponent is rather straightforward. There is one difficulty that is not readily apparent; in order to measure the maximum rate of expansion, the vector d must be along the direction of maximum expansion. In the infinite time cases, this was also true; however, there was plenty of time for d to evolve to be pointing in the proper direction and the time at the beginning during which it was not appears simply as transience. In the finite time case, however, d must begin on, or very near, the direction of maximum expansion. To find this direction, one can either solve for it analytically by maximizing the time rate of change of d given by equation 6, or evolve it as in one of the infinite time methods, realizing that data from the beginning of the simulation will not be valid.
Such a finite time method does give a characterization of how chaotic different sections of a system are, however, even this is a finite average and does not give the behavior at a specific location. Another consideration when doing numerical simulations is their efficiency. In general, it is more efficient to take a long time step than a short one. Using this algorithm, finding a more localized measure of chaos requires using a small value of t , which implies taking smaller time steps. In the case of problems like stability of celestial orbits, the most efficient integrators use time steps that are a large fraction of an orbital period. If there were short period fluctuations of the divergence rate, they would be averaged out by such methods. In response to such problems, we turn to local or zero time Lyapunov exponents. The objective here is to replace the limit as time goes to infinity in equation 1 with a limit as time goes to zero as shown here:
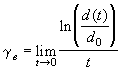 . (9)
. (9)
This was done by Eckhardt and Yao (1993) as a definition of the local Lyapunov exponent. This is equivalent to Neseís finite time definition where t is set to zero. Because plain computational methods break down here, another method must be found for evaluating this expression. To see how this works, we can rewrite equation 6 in matrix form to get
![]() , (10)
, (10)
where ![]() . If one integrates equation 10 to the first order in t, takes the norm, then expands the logarithm in equation 9, the result is an applicable form of the local Lyapunov exponent:
. If one integrates equation 10 to the first order in t, takes the norm, then expands the logarithm in equation 9, the result is an applicable form of the local Lyapunov exponent:
![]() , (11)
, (11)
where ee(x(t)) is the direction of maximum expansion at x(t). Again, finding ee has its difficulties, but once this has been done a value of the local Lyapunov exponent can be calculated. Equation 11 can be described qualitatively as the projection of L
along the direction of greatest expansion. In essence, we are simplifying equation 10 down to ![]() , where all values are the scalar magnitudes of the tensors projected along ee. The solution to this equation is instantly seen to be an exponential with growth rate g
e.
, where all values are the scalar magnitudes of the tensors projected along ee. The solution to this equation is instantly seen to be an exponential with growth rate g
e.
The Lorenz Equations: an Example
Now that the concepts have been introduced, it is instructive to look at a simple example. For this example we will use what is probably the most famous chaotic system, the Lorenz equations. Created by Edward Lorenz in 1960, this simple system of differential equations was meant to model a rather idealized convective atmosphere (Gleick, 1987). This system was selected both because it is so well known, and because it is used as an example in the papers by both Nese (1989) and Eckhardt (1993). The differential equations describing this system are as follows:
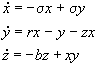 , (12)
, (12)
where s , r, and b are parameters of the system. Following with the previous papers, these were assigned values of 10, 8/3, and 28 respectively. When integrated, these equations result in the familiar butterfly shaped attractor.
A fourth order Runga-Kutta method was used to integrate these equations (code given in appendix A). Three measurements were made simultaneously during an integration of 1 million time steps using a time step of 0.01. First, a constant distance renormalization method was implemented to measure the infinite time Lyapunov exponent. This method was set to renormalize the shadow particles when they moved farther than ten times the original 0.001 separation. Figure 1 shows the time series output of this method. From this it appears that the maximum Lyapunov exponent of the Lorenz system is 0.9 inverse time units. This seems to conflict with the value of 1.3 stated in Eckhardt (1993). The reason for this disagreement is that Eckhardt is using a Lyapunov exponent with a log base two. This results in a discrepancy that is a factor of ln 2. It does however bring up an interesting question: does equation 11 also give a Lyapunov exponent based on exponential separation as a power of two? The qualitative explanation given at the end of the last section would indicate that equation 11 is based on exponential separation as a power of e, but that was only a qualitative analysis, and as none of the references I found discussed this, I can not be sure.
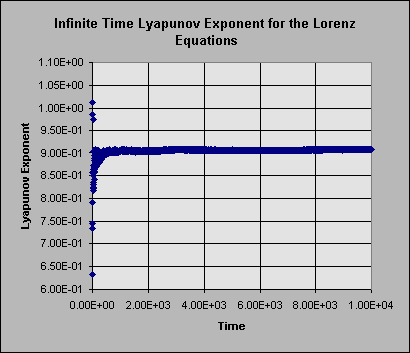
Figure 1: Infinite time Lyapunov exponent time series for an integration of the Lorenz Equations.
The second value that was measured was the finite time Lyapunov exponent, which was measured as in equation 7 with t equal to the time step of 0.01. The first ten thousand time steps were thrown away to avoid any transience in the separation vector, the remaining calculated values were binned into a grid of 100x100 and averaged over repeated hits. Figure 2 shows the results of this. Notice that the value of L is greatest in the region near the origin where one of the unstable fixed points in located. This was referred to by Nese (1989) as an area of great unpredictability. Note that in the high z region of the attractor the values L are actually are actually negative, implying that nearby orbits converge in this region and are therefore predictable.
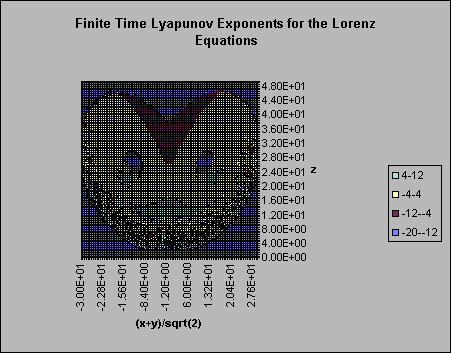
Figure 2: Finite time Lyapunov exponent grid. This displays the average values on a 100x100 grid. If the trajectory never entered a cell, a value of -35 was used.
When I first wrote the finite time Lyapunov exponent, I had it calculate values and bin them only when a renormalization was done. This had an interesting side effect as is demonstrated in Figure 3 that I didnít expect, but is perfectly understandable. The renormalizations occurred almost exclusively in the low z region. This happens because the renormalizations were done at constant distance intervals, and it is most likely to attain the proper separation while in the region of greatest separation. Renormalization was also done if the separation was reduced to 0.1 of the original separation, however, because the contraction rate is smaller than the expansion rate, this doesnít happen.
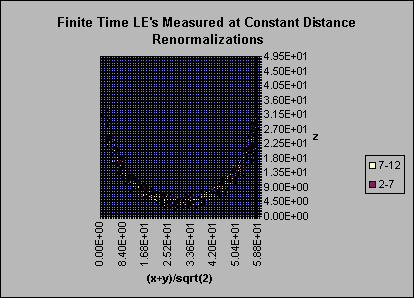
Figure 3: Finite time Lyapunov exponents binned at renormalization times. When the binning was done only at the time of a renormalization only the bins in the most chaotic region were hit.
The final measurement made during the integration was that of the local or zero time Lyapunov exponent given in equation 11. Again the first ten thousand time steps were ignored, and after that point, calculations were made at every time step using the separation vector for the direction of greatest divergence. In the case of the Lorenz system, the equation for the local Lyapunov exponent is
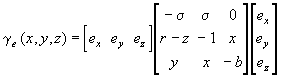 . (13)
. (13)
Using this expression in the integration and binning as described above for the finite time values produced the results seen in Figure 4.
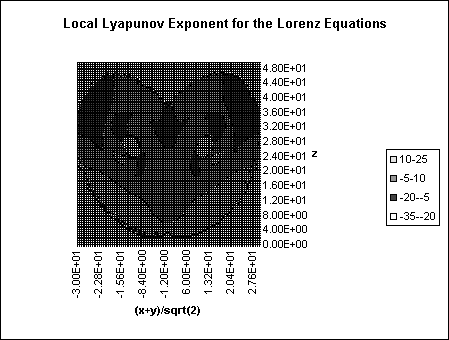
Figure 4: Local Lyapunov exponents for the Lorenz system binned as for Figure 2.
Figures 3 and 4 seem remarkably similar. This is what one would expect as Figure 4 is essentially just Figure 3 recalculated with a time step approaching zero. To better compare these results, a slightly different presentation method is used in Figure 5 to give a side by side comparison. Compare themÖ if they are of same magnitude, lends support to base e argument for zero time measure.
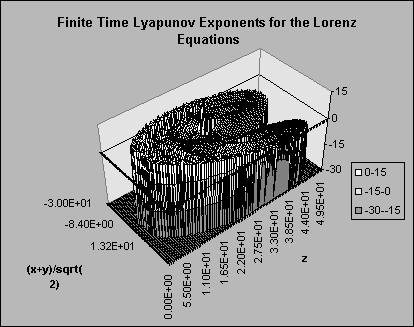
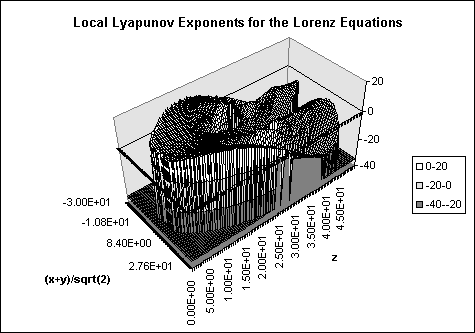
Figure 5: Comparison of finite time and zero time measurements.
Franklin-Lecar Relationship and Celestial Stability
While Poincaré was able to demonstrate that the solar system was not clockwork in the late 1800ís, very little work was done on looking at the details of the nature of chaos and stability in the solar system until the 1970ís and 1980ís. This is primarily due to the limitations of integrating celestial orbits by hand. It was not until the arrival of the computer that long term integrations became possible.
By this time, however, a great deal of physical evidence had been amassed that gave credibility to the claim that orbits in our Solar System are not stable. The most important of these being the presence of meteorites on the Earth. Such bodies are not truly "native" to the region of the solar system near the Earth. Most meteorites come from the asteroid belt and must have their regular orbits perturbed in order to be able to strike the Earth. In the 1960ís and 1970ís the question of what caused asteroids to leave their regular orbits in the region between Mars and Jupiter to swing through the inner Solar System and strike the Earth was a very puzzling one. Numerous schemes had been proposed, and while they were valid mechanisms for altering the orbits of asteroids they were all so improbable that they could not account to the number of meteorites striking the Earth. The computers of the time did allow for much longer integrations than one could do by hand, but they were still to slow to integrate the paths of such bodies for more than 10,000 years using a standard integration method. While such a period of time if large by human standards, it is really a rather short time period for things to evolve in the Solar System. As a result of their limitations, these integrations were never able to see asteroid orbits become unstable.
Certainly in time all speed limitations would have been surmounted by increases in computing power. Jack Wisdom, however, was not willing to wait. Since he couldnít increase the speed of the computer, he worked on developing more efficient integration methods. In 1983 he published a paper describing his method and what results it gave for asteroid orbits. What Wisdom did was to rely on as many features of the system as he could to simplify the math and allow larger time steps to be used in integrations. Since at the time his primary interest was in asteroid orbits, he assumed that they would follow Keplerian orbits unless acted upon by an outside force. He also assumed that perturbations that oscillated quickly would average to zero over time. Using these assumptions he was able to develop a symplectic mapping method that allowed him to follow trajectories for millions of years on existing computers. What he found when doing this was startling: the orbits of the asteroids would be regular for extended periods of time, just as other integrations had shown, but then they would undergo sudden changes in eccentricity. This showed that the orbits of asteroids could be perturbed to cross the orbit of the Earth without the use of elaborate schemes. At first many people doubted the validity of his results, saying that what he had found was an artifact of his method and not of the gravitational system. To prove that his results were correct, Wisdom accrued a large amount of computer time and redid his work using a normal integrator and found the same result.
The method that Wisdom developed in 1983 was rather limited in the scope of its applicability. This problem was solved in 1991 when he and Holman published a new symplectic mapping method that could be used for any gravitational system with a massive central body where close approaches between massive bodies didnít have to be considered. This enabled a large number of researchers to look at many different problems in celestial mechanics by doing long term integrations quickly.
In 1992 Lecar, Franklin, and Murison made an interesting discovery about the relationship between how chaotic a trajectory is as measured by the Lyapunov exponent and how long it takes for its orbit to experience a significant change, called the crossing time. They found that there is a power-law relation between these two values and have since advanced it to the form log(Tc/T0)=a+blog(Tl/T0), where Tc is the crossing time, Tl is the Lyapunov time (the inverse of the Lyapunov exponent), and T0 is either the period of the primary perturber or the particle itself (Lecar, 1996). They, and other since, have found that b seems to universally have a value around 1.7. Figure 6 shows a sample data set that I calculated for 300 orbits between Jupiter and Neptune where T0=Tj, the period of Jupiterís orbit. One of the first things you notice about this figure is how much scatter there is in the data. Obviously, the value of 1.7 has some rather large error bars on it. Some of this scatter is easily understood. Imagine if we were to take time zero to be either earlier or later down the trajectory. This would change the crossing time by whatever amount the zero time was changed, but should have no effect on the Lyapunov time.
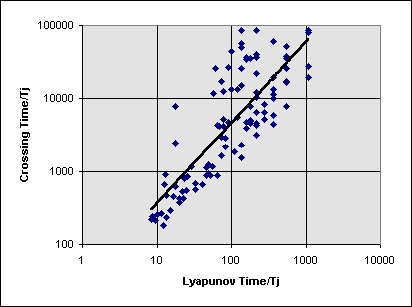
Figure 6: Plot of crossing time vs. Lyapunov time both divided by the period of Jupiter for several orbits between 6 and 30 AU from the Sun.
While this relationship is definitely interesting, the amount of scatter present in it somewhat negates its value for predicting stability from measurements of Lyapunov exponents. However, there is still some interesting physics going on here that is not yet fully understood. The next section uses measurements of the localized Lyapunov exponents to get a better understanding of why this relationship exists and give some interesting insights into the discoveries of Jack Wisdom from fifteen years ago.
Numerical Measurements of our Solar System
Finite and local Lyapunov measurements can be applied to more complex systems that the Lorenz equations. The localized chaos present in our Solar System can, for example, be measured using these same techniques. I obtained the results in this section from two sources. The time series were measured using the SWIFT code written by Harold Levison and Duncan Tremain after I added functions to renormalize at constant distance intervals and measure the finite and local Lyapunov exponents. The maps of the Lyapunov exponents over the solar system were measured with a fourth order Runga-Kutta N-body integrator which I wrote explicitly for this purpose (the code for this is contained in appendix B).
In parallel with the discussion of the Lorenz attractor given in the third section, we will first look at a time series from the measurements, then look at maps of the localized chaos over the solar system. For all of the above, the orbits of the four giant planets were integrated with a number of test particles. The measures of the various Lyapunov exponents were made on the test particles only which have zero mass. Because of this, when calculating the elements of L the variables used were position and velocity instead of position and momentum as is the standard for Hamiltonian dynamics. For a massless test particle in a system with n massive bodies, L looks like this:
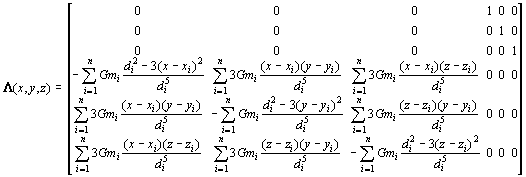 , (13)
, (13)
where di is the distance from (x,y,z) to the ith massive body, (xi,yi,zi). Figure 7 shows the infinite time average, the finite time average, and the local Lyapunov exponents, using equation 13, for a select trajectory nearly midway between Jupiter and Saturn. What first caught my attention when viewing this plot, and those of other particles as well, was that the value of the local Lyapunov exponent is much larger than that of the other two. My first reaction was to go back over the derivation of equation 13 and the code for generating these values, assuming that it was an error that generated this discrepancy. When I couldnít find any errors, I began to look for alternate explanations. When taking these measurements I had the program output values when it did the renormalizations. This is the same method that produced figure 3 for the Lorenz measurements. While in this system it is less likely that the renormalizations will occur in such localized regions of maximum separation, it will still result in measurements that are typically above the average value for the system.
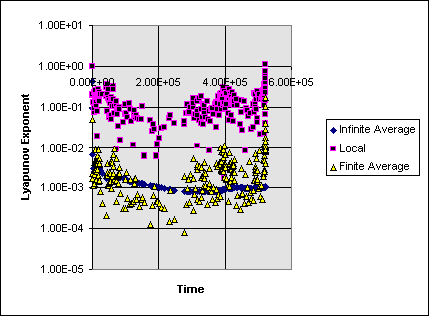
Figure 7: Time series output of the Lyapunov exponents for a particle between Jupiter and Saturn. The measurements were made and the output was done at the time that the particle and its shadow were renormalized.
By simulating a large number of particles for a period of time sufficient to allow the separation between a particle and its shadow to evolve to the direction of most rapid divergence, a map of the local and finite Lyapunov exponents was calculated. For the Lorenz equations one trajectory was followed for a long time and measurements of it were binned. Unfortunately, this method is not acceptable, even for a large number of test particles, in a gravitational system because the equations of their motion change over time as the massive bodies move. This causes many problems with coverage, because even using test particles, integrating a vast number of them for an extended period of time is prohibitively expensive in the sense of computer time. Also, because some regions of phase space are simply very unstable it is unlikely that any particles will be in such regions at the time a snap shot to the Lyapunov exponents of the system is taken. Figure 8 shows the finite and local Lyapunov exponents for the particles that remained within 30 AU of the Sun after 1000 years of evolution beginning with 1000 particles evenly distributed in circular orbits between 6 and 30 AU. To see how things change with time, Figure 9 shows an identical measurement from the same simulation after another ten years if evolution.
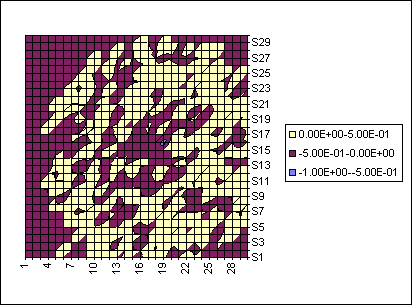
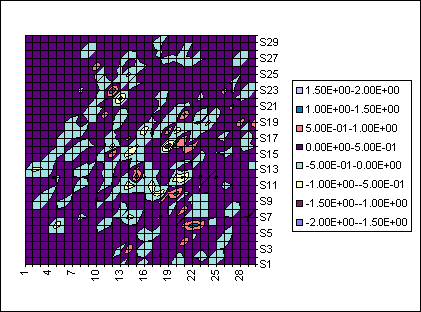

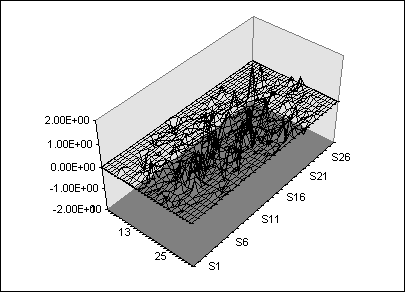
Figure 8: On the left is the finite time Lyapunov exponents and on the right the local Lyapunov exponents 1000 years into the integration of 1000 test particles.
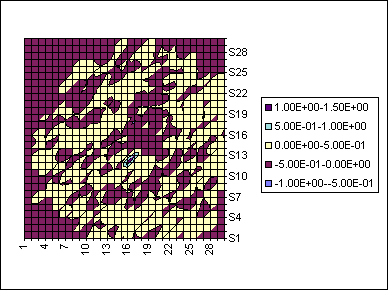
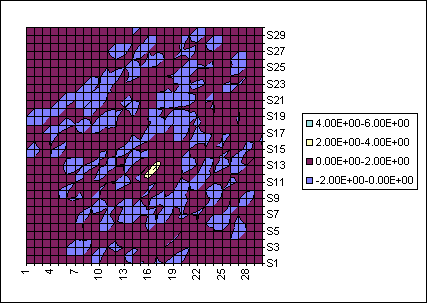


Figure 9: Same as Figure 8 from the same integration but ten years further evolved.
From the previous section we have seen that there appears to be a relationship between the infinite time Lyapunov exponent of a celestial orbit and the time period over which it is stable. The crossing time event occurs immediately after one of the sudden eccentricity jumps observed by Wisdom. It seems reasonable to then ask the question, is there any relationship between the changes in eccentricity and the local measure of eccentricity? Figure 10 shows plots similar to Figure 7 but with the eccentricity also plotted. Especially in the first plot it seems rather obvious that there is a relation between the local Lyapunov exponent and the eccentricity, though in the second plot the relationship is more difficult to discern. At this time scale is seems rather obvious that there is a relationship between these values it is not very apparent what this relationship is or why it exists.
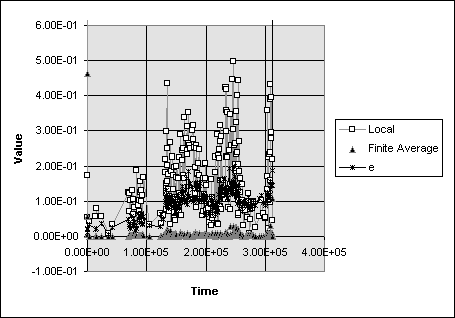
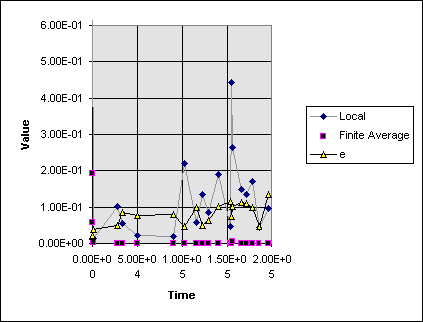
Figure 10: Local and finite time Lyapunov exponents for two particles plotted with the particles eccentricity over time. Outputs done at renormalization times. The left graph is from a particle in orbit between Jupiter and Saturn and the right is from one between Uranus and Neptune.
One problem with the data in Figure 10 is its exceedingly low temporal resolution. In an attempt to see exactly what is going on in the relationship between local Lyapunov exponents and particle eccentricity I generated a small data set for a particle writing the output at every time step. The results of this are shown in Figure 11. The first item to note in this is that it again shows a correlation between the local Lyapunov exponent and the eccentricity of the particle. In this case it appears that when the Lyapunov exponent becomes large the eccentricity gets a kick. Second there are seemingly erroneous negative Lyapunov exponents shown on this tie scale. As this is a Hamiltonian system, volumes in phase space should always be conserved, implying that the maximum Lyapunov exponent can never have a value less than zero. The reason for this apparent contradiction is fact that our phase space has two different units associated with different directions. In this case we have three coordinates measured in AU and three in AU/year. As the particle goes around the sun, if itís orbit has any eccentricity, then essentially we see distances being transferred to velocities and back. Apparently in these units volumes of space to not correspond to equal volumes of velocity. However, over the course of one orbit these inequalities are averaged out to zero.
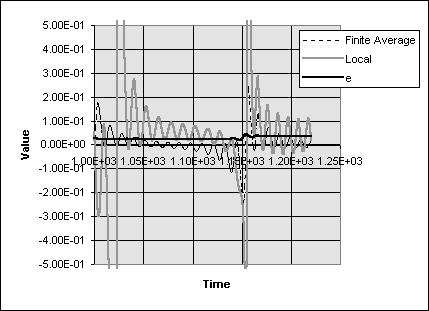
Figure 11: Comparison of the eccentricity to local and finite Lyapunov exponents. From this plot it appears that every time the Lyapunov exponents become very large the eccentricity gets a kick.
Obviously there is much more work to be done in determining the exact nature of the interaction between local Lyapunov exponents and orbital mechanics. It is possible that some parallel exists between these celestial systems and other simpler systems like the Lorenz equations. Whatever the case, local and finite time Lyapunov exponents are useful tools for the analysis of chaotic systems.
Bibliography
Eckhardt, B. and Yao, D. 1993, Physica D, 65, 100.
Geist, K., Parlitz, U., and Lauterborn, W. 1990, Progress of Theoretical Physics, 83, 875.
Gleick, J. 1987, "Chaos: Making a New Science", Penguin Books, New York, NY.
Lecar, M., Franklin, F., and Murison, M. 1992, Astronomical Journal, 104, 1230.
Lecar, M. 1996, Celestial Mechanics and Dynamical Astronomy, 64, 163.
Nese, J. 1989, Physica D, 35, 237.
Peterson, I. 1993, "Newtonís Clock: Chaos in the Solar System", W.H. Freeman and Company, New York, NY.
Tsonis, A. 1992, "Chaos from Theory to Applications", Plenum Press, New York, NY.
Wisdom, J. 1983, Icarus, 56, 51.
Wisdom, J., Holman, M. 1991, Astronomical Journal, 102, 1528.