August 9, 2012
Hi Dan,
Thank you for lying about my looks over time Dan. I only wish it were true.
And I think the Ball and Brown presentations along with the other plenary
sessions at the 2012 American Accounting Association Annual Meetings will eventually be available on the AAA Commons. Even discussants of
plenary speakers had to sign video permission forms, so our presentations may
also be available on the Commons. I was a discussant of the Deirdre McCloskey
plenary presentation on Monday, August 6. If you eventually view me on this
video you can judge how badly Dan Stone lies.
My fellow discussants were impressive, including Rob Bloomfield from Cornell,
Bill Kinney from the University of Texas (one of my former doctoral students),
and Stanimir Markov from UT. Dallas. Our moderator was Sudipta Basu from Temple
University.
The highlight of the AAA meetings for me was having an intimate breakfast
with Deirdre McCloskey. She and I had a really fine chat before four others
joined us for this breakfast hosted by the AAA prior to her plenary
presentation. What a dedicated scholar she is across decades of writing huge and
detailed history books ---
http://en.wikipedia.org/wiki/Deirdre_McCloskey
In my viewpoint she's the finest living economic historian in the world.
Sadly, she may also be one of the worst speakers in front of a large audience.
Much of this is no fault of her own, and I admire her greatly for having the
courage to speak in large convention halls. She can't be blamed for having a
rather crackling voice and a very distracting stammer. Sometimes she just cannot
get a particular word out.
My second criticism is that when making a technical presentation rather than
something like a political speech, it really does help to have a few PowerPoint
slides that highlight some the main bullet points. The AAA sets up these plenary
sessions with two very large screens and a number of other large screen
television sets that can show both the speaker's talking head and the speaker's
PowerPoint slides.
I the case of Deidre's presentation and most other technical presentations,
it really helped to have read studied her material before the presentation. For
this presentation I had carefully studied her book quoted at
The Cult of Statistical Significance: How Standard Error Costs Us Jobs,
Justice, and Lives, by Stephen T. Ziliak and Deirdre N. McCloskey (Ann
Arbor: University of Michigan Press, ISBN-13: 978-472-05007-9, 2007)
http://www.cs.trinity.edu/~rjensen/temp/DeirdreMcCloskey/StatisticalSignificance01.htm
Page 206
The textbooks are wrong. The teaching is wrong. The
seminar you just attended is wrong. The most prestigious journal in your
scientific field is wrong.
You are searching, we know, for ways to avoid being
wrong. Science, as Jeffreys said, is mainly a series of approximations to
discovering the sources of error. Science is a systematic way of reducing
wrongs or can be. Perhaps you feel frustrated by the random epistemology of
the mainstream and don't know what to do. Perhaps you've been sedated by
significance and lulled into silence. Perhaps you sense that the power of a
Roghamsted test against a plausible Dublin alternative is statistically
speaking low but you feel oppressed by the instrumental variable one should
dare not to wield. Perhaps you feel frazzled by what Morris Altman (2004)
called the "social psychology rhetoric of fear," the deeply embedded path
dependency that keeps the abuse of significance in circulation. You want to
come out of it. But perhaps you are cowed by the prestige of Fisherian
dogma. Or, worse thought, perhaps you are cynically willing to be corrupted
if it will keep a nice job
She is now writing a sequel to that book, and I cannot wait.
A second highlight for me in these 2012 AAA annual meetings was a single
sentence in the Tuesday morning plenary presentation of Gergory S. Berns, the
Director of the (Brain) Center for Neuropolicy at Emory University. In that
presentation, Dr. Berns described how the brain is divided up into over 10,000
sectors that are then studied in terms of blood flow (say from reward or
punishment) in a CAT Scan. The actual model used is the ever-popular General
Linear Model (GLM) regression equation.
The sentence in question probably passed over almost everybody's head in the
audience but mine. He discussed how sample sizes are so large in these brain
studies that efforts are made to avoid being mislead by obtaining
statistically significant GLM coefficients (due to large sample sizes) that are
not substantively significant. BINGO! Isn't this
exactly what Deidre McCloskey was warning about in her plenary session a day
earlier?
This is an illustration of a real scientist knowing what statistical
inference dangers lurk in large samples --- dangers that so many of our
accountics scientist researchers seemingly overlook as they add those Pearson
asterisks of statistical significance to questionable findings of substance in
their research.
And Dr. Berns did not mention this because he was reminded of this danger in
Deirdre's presentation the day before. Dr. Berns was not at the meetings the day
before and did not listen to Dierdre's presentation. Great scientists have
learned to be especially knowledgeable of the limitations of statistical
significance testing --- which is really intended more for small samples rather
than very large samples are used in capital markets studies by accountics
scientists.
Eight Econometrics Multiple-Choice Quiz Sets from David Giles
You might have to go to his site to get the quizzes to work.
Note that there are multiple questions for each quiz set.
Click on the arrow button to go to a subsequent question.
O.K., I know - that was a really
cheap way of getting your attention.
However, it worked, and
this post really is about
Hot Potatoes
- not the edible variety, but some
teaching apps. from "Half-Baked Software" here at the University
of Victoria.
To quote:
"The Hot
Potatoes suite
includes six applications, enabling you to create interactive
multiple-choice, short-answer, jumbled-sentence, crossword,
matching/ordering and gap-fill exercises for the World Wide Web.
Hot Potatoes is
freeware,
and you may use it for any purpose or project you like."
I've included some Hot
Potatoes multiple choice exercises on the web pages for
several of my courses for some years now. Recently, some of the
students in my introductory graduate econometrics course
mentioned that these exercises were quite helpful. So, I thought
I'd share the Hot Potatoes apps. for that course with
readers of this blog.
There are eight multiple-choice
exercise sets in total, and you can run them from here:
I've also put the HTML and associated PDF
files on the
code page
for this blog. If you're going to download
them and use them on your own computer or website, just make sure
that the PDF files are located in the same folder (directory) as the
HTML files.
I plan to extend and update these Hot Potatoes exercises in
the near future, but hopefully some readers will find them useful in
the meantime.
From my "Recently Read" list:
-
Born, B. and J. Breitung, 2014. Testing for serial correlation
in fixed-effects panel data models. Econometric Reviews, in
press.
-
Enders, W. and Lee. J., 2011. A unit root test using a Fourier
series to approximate smooth breaks, Oxford Bulletin of Economics and
Statistics, 74, 574-599.
-
Götz, T. B. and A. W. Hecq, 2014. Testing for Granger causality
in large mixed-frequency VARs. RM/14/028, Maastricht University, SBE,
Department of Quantitative Economics.
-
Kass, R. E., 2011. Statistical
inference: The big picture.
Statistical Science, 26, 1-9.
-
Qian, J. and L. Su, 2014. Structural change estimation in time
series regressions with endogenous variables. Economics Letters,
in press.
-
Wickens,
M., 2014. How did we get to where we are now? Reflections on 50
years of macroeconomic and financial econometrics. Discussion No. 14/17,
Department of Economics and Related Studies, University of York.
Statistical Science Reading List for June 2014 Compiled by David Giles in
Canada ---
http://davegiles.blogspot.com/2014/05/june-reading-list.html
Put away that novel! Here's some really fun June reading:
-
Berger, J.,
2003. Could Fisher, Jeffreys and Neyman have agreed on testing?.
Statistical Science, 18, 1-32.
-
Canal, L. and R. Micciolo, 2014. The chi-square controversy.
What if Pearson had R? Journal of Statistical Computation and
Simulation, 84, 1015-1021.
-
Harvey, D. I., S. J. Leybourne, and A. M. R. Taylor, 2014. On
infimum Dickey-Fuller unit root tests allowing for a trend break under
the null. Computational Statistics and Data Analysis, 78,
235-242.
-
Karavias, Y. and E. Tzavalis, 2014. Testing for unit roots in
short panels allowing for a structural breaks. Computational
Statistics and Data Analysis, 76, 391-407.
-
King, G.
and M. E. Roberts, 2014. How robust standard errors expose
methodological problems they do not fix, and what to do about it.
Mimeo., Harvard University.
-
Kuroki, M. and J. Pearl, 2014. Measurement bias and effect
restoration in causal inference. Biometrika, 101, 423-437.
-
Manski, C., 2014.
Communicating uncertainty in official economic statistics. Mimeo.,
Department of Economics, Northwestern University.
-
Martinez-Camblor, P., 2014. On correlated z-values in hypothesis
testing. Computational
Statistics and Data Analysis,
in press.
"Econometrics and 'Big Data'," by David Giles, Econometrics
Beat: Dave Giles’ Blog, University of Victoria, December 5, 2013 ---
http://davegiles.blogspot.ca/2013/12/econometrics-and-big-data.html
In this age of "big data" there's a whole
new language that econometricians need to learn. Its origins are
somewhat diverse - the fields of statistics, data-mining, machine
learning, and that nebulous area called "data science".
What do you know about such things as:
- Decision trees
- Support vector machines
- Neural nets
- Deep learning
- Classification and regression trees
- Random forests
- Penalized regression (e.g.,
the lasso, lars, and elastic nets)
- Boosting
- Bagging
- Spike and slab regression?
Probably not enough!
If you want some motivation to rectify
things, a recent paper by
Hal Varian will do the trick. It's titled,
"Big Data: New Tricks for Econometrics", and you can download it from
here. Hal provides an extremely readable introduction to several
of these topics.
He also offers a valuable piece of
advice:
"I believe that these methods have a lot
to offer and should be more widely known and used by economists. In
fact, my standard advice to graduate students these days is 'go to the
computer science department and take a class in machine learning'."
Interestingly, my son (a computer science
grad.) "audited" my classes on Bayesian econometrics when he was taking
machine learning courses. He assured me that this was worthwhile - and I
think he meant it! Apparently there's the potential for synergies in
both directions.
"Statistical Significance - Again " by David Giles, Econometrics
Beat: Dave Giles’ Blog, University of Victoria, December 28, 2013 ---
http://davegiles.blogspot.com/2013/12/statistical-significance-again.html
Statistical Significance - Again
With all of this emphasis
on "Big Data", I was pleased to see
this post on the Big Data
Econometrics blog, today.
When you have a sample that runs
to the thousands (billions?), the conventional significance
levels of 10%, 5%, 1% are completely inappropriate. You need to
be thinking in terms of tiny significance levels.
I discussed this in some
detail back in April of 2011, in a post titled, "Drawing
Inferences From Very Large Data-Sets".
If you're of those (many) applied
researchers who uses large cross-sections of data, and then
sprinkles the results tables with asterisks to signal
"significance" at the 5%, 10% levels, etc., then I urge
you read that earlier post.
It's sad to encounter so many
papers and seminar presentations in which the results, in
reality, are totally insignificant!
Also see
"Drawing Inferences From Very Large Data-Sets," by David Giles,
Econometrics
Beat: Dave Giles’ Blog, University of Victoria, April 26, 2013 ---
http://davegiles.blogspot.ca/2011/04/drawing-inferences-from-very-large-data.html
. . .
Granger (1998;
2003 ) has
reminded us that if the sample size is sufficiently large, then it's
virtually impossible not to reject almost any hypothesis.
So, if the sample is very large and the p-values associated with
the estimated coefficients in a regression model are of the order of, say,
0.10 or even 0.05, then this really bad news. Much,
much, smaller p-values are needed before we get all excited about
'statistically significant' results when the sample size is in the
thousands, or even bigger. So, the p-values reported above are
mostly pretty marginal, as far as significance is concerned. When you work
out the p-values for the other 6 models I mentioned, they range
from to 0.005 to 0.460. I've been generous in the models I selected.
) has
reminded us that if the sample size is sufficiently large, then it's
virtually impossible not to reject almost any hypothesis.
So, if the sample is very large and the p-values associated with
the estimated coefficients in a regression model are of the order of, say,
0.10 or even 0.05, then this really bad news. Much,
much, smaller p-values are needed before we get all excited about
'statistically significant' results when the sample size is in the
thousands, or even bigger. So, the p-values reported above are
mostly pretty marginal, as far as significance is concerned. When you work
out the p-values for the other 6 models I mentioned, they range
from to 0.005 to 0.460. I've been generous in the models I selected.
Here's another set of results taken from a second, really nice, paper by
Ciecieriski et al. (2011) in the same issue of
Health Economics:
Continued in article
Jensen Comment
My research suggest that over 90% of the recent papers published in TAR use
purchased databases that provide enormous sample sizes in those papers. Their
accountics science authors keep reporting those meaningless levels of
statistical significance.
What is even worse is when meaningless statistical significance tests are
used to support decisions.
Also see
"Drawing Inferences From Very Large Data-Sets," by David Giles,
Econometrics
Beat: Dave Giles’ Blog, University of Victoria, April 26, 2013 ---
http://davegiles.blogspot.ca/2011/04/drawing-inferences-from-very-large-data.html
. . .
Granger (1998;
2003 ) has
reminded us that if the sample size is sufficiently large, then it's
virtually impossible not to reject almost any hypothesis.
So, if the sample is very large and the p-values associated with
the estimated coefficients in a regression model are of the order of, say,
0.10 or even 0.05, then this really bad news. Much,
much, smaller p-values are needed before we get all excited about
'statistically significant' results when the sample size is in the
thousands, or even bigger. So, the p-values reported above are
mostly pretty marginal, as far as significance is concerned. When you work
out the p-values for the other 6 models I mentioned, they range
from to 0.005 to 0.460. I've been generous in the models I selected.
) has
reminded us that if the sample size is sufficiently large, then it's
virtually impossible not to reject almost any hypothesis.
So, if the sample is very large and the p-values associated with
the estimated coefficients in a regression model are of the order of, say,
0.10 or even 0.05, then this really bad news. Much,
much, smaller p-values are needed before we get all excited about
'statistically significant' results when the sample size is in the
thousands, or even bigger. So, the p-values reported above are
mostly pretty marginal, as far as significance is concerned. When you work
out the p-values for the other 6 models I mentioned, they range
from to 0.005 to 0.460. I've been generous in the models I selected.
Here's another set of results taken from a second, really nice, paper by
Ciecieriski et al. (2011) in the same issue of
Health Economics:
Continued in article
Jensen Comment
My research suggest that over 90% of the recent papers published in TAR use
purchased databases that provide enormous sample sizes in those papers. Their
accountics science authors keep reporting those meaningless levels of
statistical significance.
What is even worse is when meaningless statistical significance tests are
used to support decisions.
Question
In statistics what is a "winsorized mean?"
Answer in Wikipedia ---
http://en.wikipedia.org/wiki/Winsorized_mean
An analogy that takes me back to my early years of factor analysis is
Procreates Analysis ---
http://en.wikipedia.org/wiki/Procrustes_analysis
"The Role of Financial Reporting Quality in Mitigating the Constraining
Effect of Dividend Policy on Investment Decisions"
Authors
Santhosh Ramalingegowda (The University of Georgia
Chuan-San Wang (National Taiwan University)
Yong Yu (The University of Texas at Austin)
The Accounting Review, Vol. 88, No. 3, May 2013, pp. 1007-1040
Miller and Modigliani's (1961) dividend irrelevance
theorem predicts that in perfect capital markets dividend policy should not
affect investment decisions. Yet in imperfect markets, external funding
constraints that stem from information asymmetry can force firms to forgo
valuable investment projects in order to pay dividends. We find that
high-quality financial reporting significantly mitigates the negative effect
of dividends on investments, especially on R&D investments. Further, this
mitigating role of financial reporting quality is particularly important
among firms with a larger portion of firm value attributable to growth
options. In addition, we show that the mitigating role of high-quality
financial reporting is more pronounced among firms that have decreased
dividends than among firms that have increased dividends. These results
highlight the important role of financial reporting quality in mitigating
the conflict between firms' investment and dividend decisions and thereby
reducing the likelihood that firms forgo valuable investment projects in
order to pay dividends.
. . .
Panel A of Table 1 reports the descriptive
statistics of our main and control variables in Equation (1). To mitigate
the influence of potential outliers, we winsorize all continuous
variables at the 1 percent and 99 percent levels. The mean and median
values of Total Investment are 0.14 and 0.09 respectively. The mean and
median values of R&D Investment (Capital Investment) are 0.05 (0.06) and
0.00 (0.04), respectively. Because we multiply RQ−1 by −1 so that higher RQ−1
indicates higher reporting quality, RQ−1 has negative values with the mean
and median of −0.05 and −0.04, respectively. The above distributions are
similar to prior research (e.g., Biddle et al. 2009). The mean and median
values of Dividend are 0.01 and 0.00, respectively, consistent with many
sample firms not paying any dividends. The descriptive statistics of control
variables are similar to prior research (e.g., Biddle et al. 2009). Panels B
and C of Table 1 report the Pearson and Spearman correlations among our
variables. Consistent with dividends having a constraining effect on
investments (Brav et al. 2005; Daniel et al. 2010), we find that Total
Investment and R&D Investment are significantly negatively correlated with
Dividend.
Continued in article
Jensen Comment
With statistical inference testing on such an enormous sample size this may be
yet another accountics science illustration of misleading statistical inferences
that Deirdre McCloskey warned about (The Cult of Statistical Significance)
in a plenary session at the 2011 AAA annual meetings in 2012 ---
http://www.cs.trinity.edu/~rjensen/temp/DeirdreMcCloskey/StatisticalSignificance01.htm
I had the privilege to be one of the discussants of her amazing presentation.
The basic problem of statistical inference testing on enormous samples is
that the null hypothesis is almost always rejected even when departures from the
null are infinitesimal.
2012 AAA Meeting Plenary
Speakers and Response Panel Videos ---
http://commons.aaahq.org/hives/20a292d7e9/summary
I think you have to be a an AAA member and log into the AAA Commons to view
these videos.
Bob Jensen is an obscure speaker following the handsome Rob Bloomfield
in the 1.02 Deirdre McCloskey Follow-up Panel—Video ---
http://commons.aaahq.org/posts/a0be33f7fc
My
threads on Deidre McCloskey and my own talk are at
http://www.cs.trinity.edu/~rjensen/temp/DeirdreMcCloskey/StatisticalSignificance01.htm
September 13, 2012 reply
from Jagdish Gangolly
Bob,
Thanks you so much for posting this.
What a wonderful speaker Deidre McCloskey! Reminded
me of JR Hicks who also was a stammerer. For an economist, I was amazed by
her deep and remarkable understanding of statistics.
It was nice to hear about Gossett, perhaps the only
human being who got along well with both Karl Pearson and R.A. Fisher,
getting along with the latter itself a Herculean feat.
Gosset was helped in the mathematical derivation of
small sample theory by Karl Pearson, he did not appreciate its importance,
it was left to his nemesis R.A. Fisher. It is remarkable that he could work
with these two giants who couldn't stand each other.
In later life Fisher and Gosset parted ways in that
Fisher was a proponent of randomization of experiments while Gosset was a
proponent of systematic planning of experiments and in fact proved
decisively that balanced designs are more precise, powerful and efficient
compared with Fisher's randomized experiments (see
http://sites.roosevelt.edu/sziliak/files/2012/02/William-S-Gosset-and-Experimental-Statistics-Ziliak-JWE-2011.pdf
)
I remember my father (who designed experiments in
horticulture for a living) telling me the virtues of balanced designs at the
same time my professors in school were extolling the virtues of
randomisation.
In Gosset we also find seeds of Bayesian thinking
in his writings.
While I have always had a great regard for Fisher
(visit to the tree he planted at the Indian Statistical Institute in
Calcutta was for me more of a pilgrimage), I think his influence on the
development of statistics was less than ideal.
Regards,
Jagdish
Jagdish S. Gangolly
Department of Informatics College of Computing & Information
State University of New York at Albany
Harriman Campus, Building 7A, Suite 220
Albany, NY 12222 Phone: 518-956-8251, Fax: 518-956-8247
Hi Jagdish,
You're one of the few people who can really appreciate Deidre's scholarship in
history, economics, and statistics. When she stumbled for what seemed like
forever trying to get a word out, it helped afterwards when trying to remember
that word.
Interestingly, two Nobel economists slugged out the very essence of theory some
years back. Herb Simon insisted that the purpose of theory was to explain.
Milton Friedman went off on the F-Twist tangent saying that it was enough if a
theory merely predicted. I lost some (certainly not all) respect for Friedman
over this. Deidre, who knew Milton, claims that deep in his heart, Milton did
not ultimately believe this to the degree that it is attributed to him. Of
course Deidre herself is not a great admirer of Neyman, Savage, or Fisher.
Friedman's essay
"The
Methodology of Positive Economics" (1953) provided
the
epistemological pattern for his own subsequent
research and to a degree that of the Chicago School. There he argued that
economics as science should be free of value judgments for it to be
objective. Moreover, a useful economic theory should be judged not by its
descriptive realism but by its simplicity and fruitfulness as an engine of
prediction. That is, students should measure the accuracy of its
predictions, rather than the 'soundness of its assumptions'. His argument
was part of an ongoing debate among such statisticians as
Jerzy Neyman,
Leonard Savage, and
Ronald Fisher.
.
Many of us on the AECM are not great admirers of positive economics ---
http://www.trinity.edu/rjensen/theory02.htm#PostPositiveThinking
Everyone
is entitled to their own opinion, but not their own facts.
Senator Daniel Patrick Moynihan --- FactCheck.org ---
http://www.factcheck.org/
Then again, maybe we're all
entitled to our own facts!
"The Power of Postpositive
Thinking," Scott McLemee,
Inside Higher Ed, August 2, 2006 ---
http://www.insidehighered.com/views/2006/08/02/mclemee
In particular,
a dominant trend in critical theory was the rejection of the concept of
objectivity as something that rests on a more or less naive
epistemology: a simple belief that “facts” exist in some pristine state
untouched by “theory.” To avoid being naive, the dutiful student learned
to insist that, after all, all facts come to us embedded in various
assumptions about the world. Hence (ta da!) “objectivity” exists only
within an agreed-upon framework. It is relative to that framework. So it
isn’t really objective....
What Mohanty
found in his readings of the philosophy of science were much less naïve,
and more robust, conceptions of objectivity than the straw men being
thrashed by young Foucauldians at the time. We are not all prisoners of
our paradigms. Some theoretical frameworks permit the discovery of new
facts and the testing of interpretations or hypotheses. Others do not.
In short, objectivity is a possibility and a goal — not just in the
natural sciences, but for social inquiry and humanistic research as
well.
Mohanty’s major
theoretical statement on PPR arrived in 1997 with Literary Theory and
the Claims of History: Postmodernism, Objectivity, Multicultural
Politics (Cornell University Press). Because poststructurally
inspired notions of cultural relativism are usually understood to be
left wing in intention, there is often a tendency to assume that
hard-edged notions of objectivity must have conservative implications.
But Mohanty’s work went very much against the current.
“Since the
lowest common principle of evaluation is all that I can invoke,” wrote
Mohanty, complaining about certain strains of multicultural relativism,
“I cannot — and consequently need not — think about how your space
impinges on mine or how my history is defined together with yours. If
that is the case, I may have started by declaring a pious political
wish, but I end up denying that I need to take you seriously.”
PPR did
not require throwing out the multicultural baby with the relativist
bathwater, however. It meant developing ways to think about cultural
identity and its discontents. A number of Mohanty’s students and
scholarly colleagues have pursued the implications of postpositive
identity politics.
I’ve written elsewhere
about Moya, an associate professor of English at Stanford University who
has played an important role in developing PPR ideas about identity. And
one academic critic has written
an interesting review essay
on early postpositive scholarship — highly recommended for anyone with a
hankering for more cultural theory right about now.
Not everybody
with a sophisticated epistemological critique manages to turn it into a
functioning think tank — which is what started to happen when people in
the postpositive circle started organizing the first Future of Minority
Studies meetings at Cornell and Stanford in 2000. Others followed at the
University of Michigan and at the University of Wisconsin in Madison.
Two years ago FMS applied for a grant from Mellon Foundation, receiving
$350,000 to create a series of programs for graduate students and junior
faculty from minority backgrounds.
The FMS Summer
Institute, first held in 2005, is a two-week seminar with about a dozen
participants — most of them ABD or just starting their first
tenure-track jobs. The institute is followed by a much larger colloquium
(the part I got to attend last week). As schools of thought in the
humanities go, the postpositivists are remarkably light on the in-group
jargon. Someone emerging from the Institute does not, it seems, need a
translator to be understood by the uninitated. Nor was there a dominant
theme at the various panels I heard.
Rather, the
distinctive quality of FMS discourse seems to derive from a certain very
clear, but largely unstated, assumption: It can be useful for scholars
concerned with issues particular to one group to listen to the research
being done on problems pertaining to other groups.
That sounds
pretty simple. But there is rather more behind it than the belief that
we should all just try to get along. Diversity (of background, of
experience, of disciplinary formation) is not something that exists
alongside or in addition to whatever happens in the “real world.” It is
an inescapable and enabling condition of life in a more or less
democratic society. And anyone who wants it to become more democratic,
rather than less, has an interest in learning to understand both its
inequities and how other people are affected by them.
A case in point
might be the findings discussed by Claude Steele, a professor of
psychology at Stanford, in a panel on Friday. His paper reviewed some of
the research on “identity contingencies,” meaning “things you have to
deal with because of your social identity.” One such contingency is what
he called “stereotype threat” — a situation in which an individual
becomes aware of the risk that what you are doing will confirm some
established negative quality associated with your group. And in keeping
with the threat, there is a tendency to become vigilant and defensive.
Steele did not
just have a string of concepts to put up on PowerPoint. He had research
findings on how stereotype threat can affect education. The most
striking involved results from a puzzle-solving test given to groups of
white and black students. When the test was described as a game, the
scores for the black students were excellent — conspicuously higher, in
fact, than the scores of white students. But in experiments where the
very same puzzle was described as an intelligence test, the results were
reversed. The black kids scores dropped by about half, while the graph
for their white peers spiked.
The only
variable? How the puzzle was framed — with distracting thoughts about
African-American performance on IQ tests creating “stereotype threat” in
a way that game-playing did not.
Steele also
cited an experiment in which white engineering students were given a
mathematics test. Just beforehand, some groups were told that Asian
students usually did really well on this particular test. Others were
simply handed the test without comment. Students who heard about their
Asian competitors tended to get much lower scores than the control
group.
Extrapolate
from the social psychologist’s experiments with the effect of a few
innocent-sounding remarks — and imagine the cumulative effect of more
overt forms of domination. The picture is one of a culture that is
profoundly wasteful, even destructive, of the best abilities of many of
its members.
“It’s not easy
for minority folks to discuss these things,” Satya Mohanty told me on
the final day of the colloquium. “But I don’t think we can afford to
wait until it becomes comfortable to start thinking about them. Our
future depends on it. By ‘our’ I mean everyone’s future. How we enrich
and deepen our democratic society and institutions depends on the
answers we come up with now.”
Earlier this year, Oxford
University Press published a major new work on postpositivist theory,
Visible Identities: Race, Gender, and the Self,by Linda Martin
Alcoff, a professor of philosophy at Syracuse University. Several essays
from the book are available at
the author’s
Web site.
Steve Kachelmeier wrote the following on May 7, 2012
I like to pose this question to first-year doctoral
students: Two researchers test a null hypothesis using a classical
statistical approach. The first researcher tests a sample of 20 and the
second tests a sample of 20,000. Both find that they can reject the null
hypothesis at the same exact "p-value" of 0.05. Which researcher can say
with greater confidence that s/he has found a meaningful departure from the
null?
The vast majority of doctoral students respond that
the researcher who tested 20,000 can state the more meaningful conclusion. I
then need to explain for about 30 minutes how statistics already dearly
penalizes the small-sample-size researcher for the small sample size, such
that a much bigger "effect size" is needed to generate the same p-value.
Thus, I argue that the researcher with n=20 has likely found the more
meaningful difference. The students give me a puzzled look, but I hope they
(eventually) get it.
The moral? As I see it, the problem is not so much
whether we use classical or Bayesian statistical testing. Rather, the
problem is that we grossly misinterpret the word "significance" as meaning
"big," "meaningful," or "consequential," when in a statistical sense it only
means "something other than zero."
In Accountics Science R2 = 0.0004 =
(-.02)(-.02) Can Be Deemed a Statistically Significant Linear Relationship
"Disclosures of Insider Purchases and the Valuation Implications of Past
Earnings Signals," by David Veenman, The Accounting Review, January 2012
---
http://aaajournals.org/doi/full/10.2308/accr-10162
. . .
Table 2 presents descriptive statistics for the
sample of 12,834 purchase filing observations. While not all market
responses to purchase filings are positive (the Q1 value of CAR% equals
−1.78 percent), 25 percent of filings are associated with a market reaction
of at least 5.32 percent. Among the main variables, AQ and AQI have mean
(median) values of 0.062 (0.044) and 0.063 (0.056), respectively. By
construction, the average of AQD is approximately zero. ΔQEARN and ΔFUTURE
are also centered around zero.
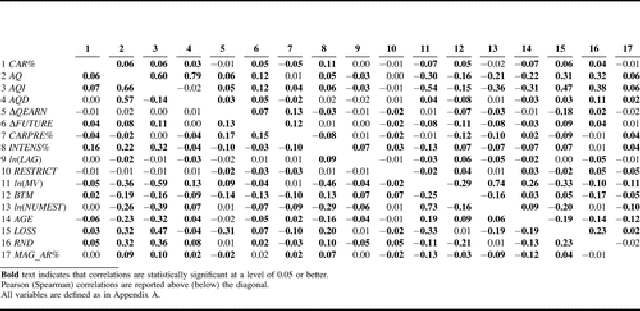
Jensen Comment
Note that correlations shown in bold face type are deemed statistically
significant a .05 level. I wonder what it tells me when a -0.02 correlation is
statistically significant at a .05 level and a -0.01 correlation is not
significant? I have similar doubts about the distinctions between "statistical
significance" in the subsequent tables that compare .10, .05, and .01 levels of
significance.
Especially note that if David Veenman sufficiently increased the sample
size both -.00002 and -.00001 correlations might be made to be
statistically significant.
Just so David Veenman does not think I only singled him out for illustrative
purposes
In Accountics Science R2 = 0.000784 =
(-.028)(-.028) Can Be Deemed a Statistically Significant Linear Relationship
"Cover Me: Managers' Responses to Changes in Analyst Coverage in the
Post-Regulation FD Period," by Divya Anantharaman and Yuan Zhang, The
Accounting Review, November 2011 ---
http://aaajournals.org/doi/full/10.2308/accr-10126
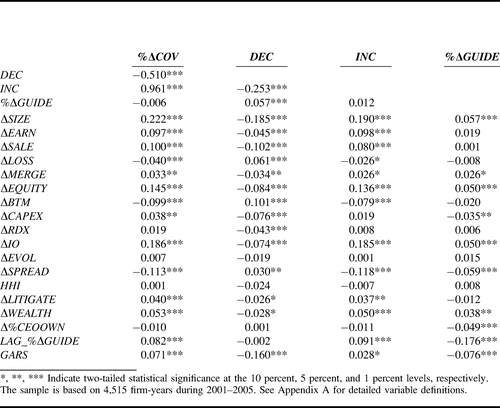
I might have written a commentary about this and submitted it to The
Accounting Review (TAR), but 574 referees at TAR will not publish critical
commentaries of papers previously published in TAR ---
http://www.trinity.edu/rjensen/TheoryTAR.htm
How Accountics Scientists Should Change:
"Frankly, Scarlett, after I get a hit for my resume in The Accounting Review
I just don't give a damn"
http://www.cs.trinity.edu/~rjensen/temp/AccounticsDamn.htm
One more mission in what's left of my life will be to try to change this
http://www.cs.trinity.edu/~rjensen/temp/AccounticsDamn.htm
The Cult of Statistical Significance: How Standard Error Costs Us
Jobs, Justice, and Lives, by Stephen T. Ziliak and Deirdre N. McCloskey
(Ann Arbor: University of Michigan Press, ISBN-13: 978-472-05007-9, 2007)
Page 206
Like scientists today in medical and economic and
other sizeless sciences, Pearson mistook a large sample size for the
definite, substantive significance---evidence s Hayek put it, of "wholes."
But it was as Hayek said "just an illusion." Pearson's columns of sparkling
asterisks, though quantitative in appearance and as appealing a is the
simple truth of the sky, signified nothing.
pp. xv-xvi
The implied reader of our book is a significance
tester, the keeper of numerical things. We want to persuade you of one
claim: that William Sealy Gosset (1879-1937) --- aka "Student" of
Student's t-test --- was right and that his difficult friend, Ronald A.
Fisher, though a genius, was wrong. Fit is not the same thing as
importance. Statistical significance is not the same thing as scientific
finding. R2. t-statistic, p-value, F-test, and all the more
sophisticated versions of them in time series and the most advanced
statistics are misleading at best.
No working scientist today knows much about Gosset,
a brewer of Guinness stout and the inventor of a good deal of modern
statistics. The scruffy little Gossset, with his tall leather boots and a
rucksack on his back, is the heroic underdog of our story. Gosset, we claim,
was a great scientist. He took an economic approach to the logic of
uncertainty. For over two decades he quietly tried to educate Fisher. But
Fisher, our flawed villain, erased from Gosset's inventions the consciously
economic element. We want to bring it back.
. . .
Can so many scientists have been wrong for the
eighty years since 1925? Unhappily yes. The mainstream in science, as any
scientist will tell you, is often wrong. Otherwise, come to think of it,
science would be complete. Few scientists would make that claim, or would
want to. Statistical significance is surely not the only error of modern
science, although it has been, as we will show, an exceptionally damaging
one. Scientists are often tardy in fixing basic flaws in their sciences
despite the presence of better alternatives. ...
Continued in the Preface
Page 3
A brewer of beer, William Sealy Gosset (1876-1937),
proved its (statistical significance) in small
samples. He worked at the Guinness Brewer in Dublin, where for
most of his working life he was head experimental brewer. He saw in 1905
where the need for a small-smle test because he was testing varieties of
hops and barley in field samples with N as small as four. Gosset, who is
hardly remembered nowadays, quietly invented many tools of modern applied
statistics, including Monte Carlo analysis, the balanced design of
experiments, and, especially, Student's t, which is the foundation of
small-sample theory and the most commonsly7 used test of statistical
significance in the sciences. ... But the value Gosset intended with his
test, he said without deviation from 1905 until his death in 1937. was its
ability to sharpen statements of substantive or economic
significance. ... (he) wrote to his elderly friend, the great Karl Person:
"My own war work is obviously to brew Guinness stout in each way as to waste
as little labor and material as possible, and I am hoping to help to do
something fairly creditable in that way." It seems he did.
Page 10
Sizelessness is not what most Fisherians (deciples of
Ronald Fisher) believe they are getting. The sizeless scientists have
adopted a method of deciding which numbers are significant that has little to
do with the humanly significant numbers. The scientists re counting, to be
sure: "3.14159***," they proudly report of simply "****." But, as the
probablist Bruno de Finetti said, they proudly report scientists are acting
as though "addition requires different operations if concerned with pure
number or amounts of money" (De Finetti 1971, 486, quoted in Savage 1971a).
Substituting "significance" for scientific how much
would imply that the value of a lottery ticket is the chance itself, the
chance 1 in 38,000, say in or 1 in 1,000,000,000. It supposes that the only
source in value in the lottery is sampling variability. It sets aside as
irrelevant---simply ignores---the value of the expected prize., the millions
that success in the lottery could in fact yield. Setting aside both old and
new criticisms of expected utility theory, a prize of $3.56 is very
different, other things equal, from a prize of $356,000,000. No matter.
Statistical significance, startlingly, ignores the difference.
Continued on Page 10
Page 15
The doctor who cannot distinguish statistical
significance from substantive significance, an F-statistic from a heart
attach, is like an economist who ignores opportunity cost---what statistical
theorists call the loss function. The doctors of "significance" in medicine
and economy are merely "deciding what to say rather than what to do" (Savage
1954, 159). In the 1950s Ronald Fisher published an article and a book that
intended to rid decision from the vocabulary of working statisticians
(1955, 1956). He was annoyed by the rising authority in highbrow circles of
those he called "the Neymanites."
Continued on Page 15
pp. 28-31
An example is provided regarding how Merck manipulated statistical inference
to keep its killing pain killer Vioxx from being pulled from the market.
Page 31
Another story. The Japanese government in June 2005
increased the limit on the number of whales that may be annually killed in
the Antarctica---from around 440 annually to over 1,000 annually. Deputy
Commissioner Akira Nakamae explained why: "We will implement JARPS-2
[the plan for the higher killing] according to the schedule, because the
sample size is determined in order to get statistically significant results"
(Black 2005). The Japanese hunt for the whales, they claim, in order to
collect scientific data on them. That and whale steaks. The commissioner is
right: increasing sample size, other things equal, does increase the
statistical significance of the result. It is, fter all, a mathematical fact
that statistical significance increases, other things equal, as sample size
increases. Thus the theoretical standard error of JAEPA-2, s/SQROOT(440+560)
[given for example the simple mean formula], yields more sampling precision
than the standard error JARPA-1, s/SQROOT(440). In fact it raises the
significance level to Fisher's percent cutoff. So the Japanese government
has found a formula for killing more whales, annually some 560 additional
victims, under the cover of getting the conventional level of Fisherian
statistical significance for their "scientific" studies.
pp. 250-251
The textbooks are wrong. The teaching is wrong. The
seminar you just attended is wrong. The most prestigious journal in your
scientific field is wrong.
You are searching, we know, for ways to avoid being
wrong. Science, as Jeffreys said, is mainly a series of approximations to
discovering the sources of error. Science is a systematic way of reducing
wrongs or can be. Perhaps you feel frustrated by the random epistemology of
the mainstream and don't know what to do. Perhaps you've been sedated by
significance and lulled into silence. Perhaps you sense that the power of a
Roghamsted test against a plausible Dublin alternative is statistically
speaking low but you feel oppressed by the instrumental variable one should
dare not to wield. Perhaps you feel frazzled by what Morris Altman (2004)
called the "social psychology rhetoric of fear," the deeply embedded path
dependency that keeps the abuse of significance in circulation. You want to
come out of it. But perhaps you are cowed by the prestige of Fisherian
dogma. Or, worse thought, perhaps you are cynically willing to be
corrupted if it will keep a nice job
See the review at
http://economiclogic.blogspot.com/2012/03/about-cult-of-statistical-significance.html
Costs and Benefits of Significance Testing ---
http://www.cato.org/pubs/journal/cj28n2/cj28n2-16.pdf
Jensen Comment
I'm only part way into the book and reserve judgment at this point. It seems to
me in these early stages that they overstate their case (in a very scholarly but
divisive way). However, I truly am impressed by the historical citations
in this book and the huge number of footnotes and references. The book has a
great index.
For most of my scholastic life I've argued that there's a huge difference
between significance testing versus substantive testing. The first thing I look
for when asked to review an accountics science study is the size of the samples.
But this issue is only a part of this fascinating book.
Deirdre McCloskey will kick off the American Annual Meetings in Washington DC
with a plenary session first thing in the morning on August 6, 2012. However
she's not a student of accounting. She's the Distinguished Professor of
Economics, History, English, and Communication, University of Illinois at
Chicago and to date has received four honorary degrees ---
http://www.deirdremccloskey.com/
Also see
http://en.wikipedia.org/wiki/Deirdre_McCloskey
I've been honored to be on a panel following her presentation to debate her
remarks. Her presentation will also focus on Bourgeois Dignity: Why
Economics Can't Explain the Modern World.
Steven T. Ziliac is a former professor of economics at Carnegie who is now a
Professor of Economics specializing in poverty research at Roosevelt University
---
http://en.wikipedia.org/wiki/Stephen_T._Ziliak
Would Nate Silver Touch This Probability Estimate With a 10-Foot Baysian
Pole?
"Calculating the Probabilities of a U.S. Default." by Justin Fox,
Harvard Business Review Article, October 10, 2013 ---
Click Here
http://blogs.hbr.org/2013/10/calculating-the-probabilities-of-a-u-s-default/?utm_source=feedburner&utm_medium=feed&utm_campaign=Feed%3A+harvardbusiness+%28HBR.org%29&cm_ite=DailyAlert-101113+%281%29&cm_lm=sp%3Arjensen%40trinity.edu&cm_ven=Spop-Email
An argument has been making the rounds that there’s
really no danger of default if the U.S. runs up against the debt ceiling —
the president could simply make sure that all debt payments are made on
time, even as other government bills go unpaid. I’ve heard it from economist
Thomas Sowell,
investor and big-time political donor
Foster Friess, and pundit
George Will. It’s even been made right here on
HBR.org by Tufts University accounting professor
Lawrence Weiss.
The Treasury Department has been saying all along
that
it can’t do this; it makes 80 million payments a
month, and it’s simply not technically capable of sorting out which ones to
make on time and which ones to hold off on. I don’t know if this is true,
and there may be an element of political posturing in such statements. On
the other hand, it is the Treasury Department that has to pay the bills. If
they say they’re worried, I can’t help but worry too. When Tony Fratto, who
worked in the Treasury Department in the Bush Administration,
seconds this concern, I worry even more. Not to
mention that this has happened before, in
the mini-default of 1979, when Treasury systems
went on the fritz in the wake of a brief Congressional standoff over — you
guessed it — raising the debt ceiling.
Then there’s the question of legality. The second
the President or the Treasury Secretary starts choosing which bills to pay,
he usurps the spending authority that the U.S. Constitution grants Congress.
The Constitution states, in the 14th Amendment, that the U.S. will pay its
debts. But there is no clear path to honoring this commitment in the face of
a breached debt ceiling. Writing
in the Columbia Law Review last year, Neil
H. Buchanan of George Washington University Law School and Michael C. Dorf
of Cornell University Law School concluded that as every realistic option
faced by the president violated the Constitution in some way, the “least
unconstitutional” thing to do would not be to stop making some payments but
to ignore the debt ceiling. That’s because, in comparison with unilaterally
raising taxes or cutting spending to enable the U.S. to continue making its
debt payments under the current ceiling, ignoring the debt limit would
“minimize the unconstitutional assumption of power, minimize
sub-constitutional harm, and preserve, to the extent possible, the ability
of other actors to undo or remedy constitutional violations.” And even this
option, Buchanan and Dorf acknowledge, is fraught with risk: financial
markets might shun the new bonds issued under presidential fiat as
“radioactive.”
So assigning a 0% probability to the possibility
that running into the debt ceiling will lead to some kind of default doesn’t
sound reasonable. What is reasonable? Let’s say 25%, although really
that’s just a guess. The likelihood that hitting the ceiling will result in
sustained higher interest rates for the U.S. is higher (maybe 50%?) and the
likelihood that it will temporarily raise short-term rates is something like
99.99%, since those rates have
already been rising.
It’s the kind of thing that makes you wish Nate
Silver weren’t
too busy hiring people for the new,
Disneyfied fivethirtyeight.com to focus on. At
this point even Silver would have to resort to guesswork — this is a mostly
unprecedented situation we’re dealing with here. But the updating of his
predictions as new information came in would be fascinating to watch, and
might even add some calm sanity to the discussion.
Updating is what the
Bayesian approach to statistics that Silver swears
by is all about. Reasonable people can start out with differing opinions
about the likelihood that something will happen, but as new information
comes in they should all be using the same formula (Bayes’
formula) to update their predictions, and
in the process their views should move closer together. “The role of
statistics is not to discover truth,” the late, great Bayesian Leonard
“Jimmie” Savage used to say. “The role of statistics is to resolve
disagreements among people.” (At least, that’s how his friend Milton
Friedman remembered it; the quote is from the book
Two Lucky People.)
I tread lightly here, because I’m one of those
idiots who never took a statistics class in college, so don’t expect me to
be any help on Bayesian methods. But as a philosophy, I think it can be
expressed something like this: You’re entitled to your opinion. You’re even
entitled to your opinion as to how much weight to give new information as it
comes in. But you need to be explicit about your predictions and
weightings, and willing to change your opinion if Bayes theorem tells you
to. A political environment where that was the dominant approach
would be pretty swell, no?
Not that it would resolve everything. Some
Republicans
have been making the very Bayesian argument that,
after dire predictions about the consequences of the sequester and the
government shutdown failed to come true, the argument that a debt ceiling
breach would be disastrous has become less credible. As a matter of
politics, they have a point: the White House
clearly oversold the potential economic
consequences of both sequester and shutdown. But I never took those dire
claims about the sequester and shutdown seriously, so my views on the
dangers associated with hitting the debt ceiling haven’t changed much at
all. And while I’m confident that my view is more reasonable than that of
the debt-ceiling Pollyannas, I don’t see how I can use Bayesian statistics
to convince them of that, or how they can use it to sway me. Until we hit
the debt limit.
Nate Silver ---
http://en.wikipedia.org/wiki/Nate_Silver
Jensen Comment
David Johnstone's romance with Bayesian probability, in his scholarly messages
to the AECM, prompted me once again in my old age to delve into the Second
Edition of Causality by Judea Pearl (Cambridge University press).
I like this book and can study various points raised by David. But estimating
the probability of default in the context of the above posting by Justin Fox
raises many doubts in my mind.
A Database on Each Previous Performance Outcome of a Baseball Player
The current Bayesian hero Nate Silver generally predicts from two types of
databases. His favorite database is the history of baseball statistics of
individual players when estimating the probability of performance of a current
player, especially pitching and batting performance. Fielding performances are
more difficult to predict because is such a variance of challenges for each
fielded ball. His Pecota system is based upon the statistical history of each
player.
A Sequence of Changing Databases of Election Poll Outcomes
Election polls emerge at frequent points in time (e.g., monthly). These are not
usually recorded data points of each potential voter (like data points over time
of a baseball player). But they are indicative of the aggregate outcome of all
voters who will eventually make a voting choice on election day.
The important point to note in this type of database is that the respondent
is predicting his or her own act of voting. The task is not to predict how an
act of Congress over which the respondent has no direct control and no inside
information about the decision process of individual members of Congress (who
could just be bluffing for the media).
The problem Nate has is in the chance that a significant number of voters
will change their minds back and forth write up to pulling the lever in a voting
booth. This is why Nate has some monumental prediction errors for political
voting relative to baseball player performance. One of those errors concerned in
predictions regarding the winner of the Senate Seat in Massachusetts after the
death of Ted Kennedy. Many voters seemingly changed their minds just before or
during election day.
There are no such databases for estimating the probability of USA debt
default in October of 2013.
Without a suitable database I don't think Nate Silver would estimate the
probability of USA loan default in October of 2013. This begs the question of
what Nate might do if a trustworthy poll sampled voters on their estimates of
the probability of default. I don't think Nate would trust this database,
however, because the random respondents across the USA do not have inside
information or expertise for making such probability analysis and are most
likely inconsistently informed with respect to which TV networks they watch or
newspapers they read.
I do realize that databases of economic predictions of expert economists or
expert weather forecasters have some modicum of success. But the key word here
is the adjective "expert." I'm not sure there are any experts of the
probabilities of one particular and highly circumstantial USA debt default in
October of 2013 even though there are experts on forecasting the 2013 GDP.
Bayesian probability is a formalized derivation of a person's belief.
But if there is no justification for for having some confidence in that person's
belief then there really is not much use of deriving that person's subjective
probability estimate. For example, if you asked me about my belief in regarding
the point spread in a football game next Friday night between two high schools
in Nevada my belief on the matter is totally useless because I've never
even heard of any particular high schools in Nevada let alone their football
teams.
I honestly think that what outsiders believe about the debt default issue for
October 2013 is totally useless. It might be interesting to compute Bayesian
probabilities of such default from Congressional insiders, but most persons in
Congress cannot be trusted to be truthful about their responses, and their
responses vary greatly in terms of expertise because the degree of inside
information varies so among members of Congress. This is mostly a game of
political posturing and not a game of statistics.
October 12, 2013 reply from David Johnstone
Dear Bob, I think you are on the Bayesian hook, many Bayesians say how they
started off as sceptics or without any wish for a new creed, but then got
drawn in when they saw the insights and tools that Bayes had in it. Dennis
Lindley says that he set out in his 20s to prove that something was wrong
with Bayesian thinking, but discovered the opposite. Don’t be fooled by the
fact that most business school PhD programs have in general rejected or
never discovered Bayesian methods, they similarly hold onto all sorts of
vested theoretical positions for as long as possible.
The thing about Bayes, that makes resistance amusing, is that if you accept
the laws of probability, which merely show how one probability relates
logically to another, then you have to be “Bayesian” because the theorem is
just a law of probability. Basically, you either accept Bayes and the
probability calculus, or you go into a no man’s land.
That does not mean that Bayes theorem gives answers by formal calculations
all the time. Many probabilities are just seat of the pants subjective
assessments. But (i) these are more sensible if they happen to be consistent
with other probabilities that we have assessed or hold, and (ii) they may be
very inaccurate, since such judgements are often very hard, even for
supposed experts. The Dutch Book argument that is widely used for Bayes is
that if you hold two probabilities that are mutually inconsistent by the
laws of probability, you can have bets set against you by which you will
necessarily lose, whatever the events are. This is the same way by which
bookmakers set up arbitrages against their total of bettors, so that they
win net whatever horse wins the race. The Bayesian creed is “coherence”, not
correctness. Correctness is asking too much, coherence is just asking for
consistency between beliefs.
Bayes theorem is not a religion or a pop song, it’s just a law of
probability, so romance is out of the question. And if we do conventional
“frequentist” statistics (significance tests etc.) we often break these laws
in our reasoning, which is remarkable given that we hold ourselves out as so
scientific, logical and sophisticated. It is also a cognitive dissonance
since at the same time we often start with a theoretical model of behaviour
that assumes only Bayesian agents. This is pretty hilarious really, for what
it says about people and intellectual behavior, and about how forgiving
“nature” is of us, by indulging our cognitive proclivities without stinging
us fatally for any inconsistencies.
Bayes theorem recognises that much opinion is worthless, and that shows up
in the likelihood function. For example, the probability of a head given
rain is the same as the probability of a head given fine, so a coin toss (or
equivalent “expert”) gives no help whatsoever in predicting rain. Bayes
theorem is only logic, it’s not a forecasting method of itself. While on
weather, those people are seriously good forecasters, despite their
appearance in many jokes, and leave economic forecasters for dead. Their
problems might be “easier” than forecasting markets, but they have made
genuine theoretical and practical progress. I have suggested to weather
forecasters in Australia that they should run an on-line betting site on
“rain events” and let people take them on, there would be very few who don’t
get skinned quickly.
I won’t go on more, but if I did it would be to say that it is the
principles of logic implicit in Bayes theorem that are so insightful and
helpful about it. These should have been taught to us all at school, when we
were learning deductive logic (e.g. sums). I think it is often argued that
probability was associated with gambling and uncertainty, offending many
religious and social beliefs, and hence was a bit of an underworld
historically. Funny that Thomas Bayes was a Rev.
October 13, 2013 reply from Bob Jensen
Hi David,
You're facing an enormous task
trying to change accountics scientists who trained only to apply
popular GLM statistical inference software like SAS, SPSS,
Statistica, Sysstat, and MATLAB to purchased databases like
Betty Crocker follows recipes for baking desserts. Mostly they
ignore the tremendous limitations and assumptions of the Cult of
Statistical Inference:
The Cult of Statistical Significance: How Standard Error
Costs Us Jobs, Justice, and Lives ---
http://www.cs.trinity.edu/~rjensen/temp/DeirdreMcCloskey/StatisticalSignificance01.htm
Do you have any recommendations for
Bayesian software such as WinBugs, Bayesian Filtering Library, JAGS,
Mathematica and possibly some of the Markov chain analysis software?
http://en.wikipedia.org/wiki/List_of_statistical_packages
Respectfully,
Bob Jensen
May 11, 2012 reply from Jagdish Gangolly
Hopefully this is my last post on this thread. I
just could not resist posting this appeal to editors, chairs, directors,
reviewers,... by Professor John Kruschke, Professor of Psychological and
Brain Sciences and Statistics at Indiana University.
His book on " Doing Bayesian Data Analysis: A
Tutorial with R and BUGS " is the best introductory textbook on statistics I
have read.
Regards to all,
Jagdish
Here is the open letter:
___________________________________________________
An open letter to Editors of journals, Chairs of departments,
Directors of funding programs, Directors of graduate training, Reviewers
of grants and manuscripts, Researchers, Teachers, and Students:
Statistical methods have been evolving rapidly, and many people think
it’s time to adopt modern Bayesian data analysis as standard procedure
in our scientific practice and in our educational curriculum. Three
reasons:
1. Scientific disciplines from astronomy to zoology are moving to
Bayesian data analysis. We should be leaders of the move, not followers.
2. Modern Bayesian methods provide richer information, with greater
flexibility and broader applicability than 20th century methods.
Bayesian methods are intellectually coherent and intuitive. Bayesian
analyses are readily computed with modern software and hardware.
3. Null-hypothesis significance testing (NHST), with its reliance on
p values, has many problems. There is little reason to persist with NHST
now that Bayesian methods are accessible to everyone.
My conclusion from those points is that we should do whatever we can
to encourage the move to Bayesian data analysis. Journal editors could
accept Bayesian data analyses, and encourage submissions with Bayesian
data analyses. Department chairpersons could encourage their faculty to
be leaders of the move to modern Bayesian methods. Funding agency
directors could encourage applications using Bayesian data analysis.
Reviewers could recommend Bayesian data analyses. Directors of training
or curriculum could get courses in Bayesian data analysis incorporated
into the standard curriculum. Teachers can teach Bayesian. Researchers
can use Bayesian methods to analyze data and submit the analyses for
publication. Students can get an advantage by learning and using
Bayesian data analysis.
The goal is encouragement of Bayesian methods, not prohibition of
NHST or other methods. Researchers will embrace Bayesian analysis once
they learn about it and see its many practical and intellectual
advantages. Nevertheless, change requires vision, courage, incentive,
effort, and encouragement!
Now to expand on the three reasons stated above.
1. Scientific disciplines from astronomy to zoology are moving to
Bayesian data analysis. We should be leaders of the move, not followers.
Bayesian methods are revolutionizing science. Notice the titles of
these articles:
Bayesian computation: a statistical revolution. Brooks, S.P.
Philosophical Transactions of the Royal Society of London. Series A:
Mathematical, Physical and Engineering Sciences, 361(1813), 2681, 2003.
The Bayesian revolution in genetics. Beaumont, M.A. and Rannala, B.
Nature Reviews Genetics, 5(4), 251-261, 2004.
A Bayesian revolution in spectral analysis. Gregory, PC. AIP
Conference Proceedings, 557-568, 2001.
The hierarchical Bayesian revolution: how Bayesian methods have
changed the face of marketing research. Allenby, G.M. and Bakken, D.G.
and Rossi, P.E. Marketing Research, 16, 20-25, 2004
The future of statistics: A Bayesian 21st century. Lindley, DV.
Advances in Applied Probability, 7, 106-115, 1975.
There are many other articles that make analogous points in other
fields, but with less pithy titles. If nothing else, the titles above
suggest that the phrase “Bayesian revolution” is not an overstatement.
The Bayesian revolution spans many fields of science. Notice the
titles of these articles:
Bayesian analysis of hierarchical models and its application in
AGRICULTURE. Nazir, N., Khan, A.A., Shafi, S., Rashid, A. InterStat, 1,
2009.
The Bayesian approach to the interpretation of ARCHAEOLOGICAL DATA.
Litton, CD & Buck, CE. Archaeometry, 37(1), 1-24, 1995.
The promise of Bayesian inference for ASTROPHYSICS. Loredo TJ. In:
Feigelson ED, Babu GJ, eds. Statistical Challenges in Modern Astronomy.
New York: Springer-Verlag; 1992, 275–297.
Bayesian methods in the ATMOSPHERIC SCIENCES. Berliner LM, Royle JA,
Wikle CK, Milliff RF. In: Bernardo JM, Berger JO, Dawid AP, Smith AFM,
eds. Bayesian Statistics 6: Proceedings of the sixth Valencia
international meeting, June 6–10, 1998. Oxford, UK: Oxford University
Press; 1999, 83–100.
An introduction to Bayesian methods for analyzing CHEMISTRY data::
Part II: A review of applications of Bayesian methods in CHEMISTRY.
Hibbert, DB and Armstrong, N. Chemometrics and Intelligent Laboratory
Systems, 97(2), 211-220, 2009.
Bayesian methods in CONSERVATION BIOLOGY. Wade PR. Conservation
Biology, 2000, 1308–1316.
Bayesian inference in ECOLOGY. Ellison AM. Ecol Biol 2004, 7:509–520.
The Bayesian approach to research in ECONOMIC EDUCATION. Kennedy, P.
Journal of Economic Education, 17, 9-24, 1986.
The growth of Bayesian methods in statistics and ECONOMICS since
1970. Poirier, D.J. Bayesian Analysis, 1(4), 969-980, 2006.
Commentary: Practical advantages of Bayesian analysis of
EPIDEMIOLOGIC DATA. Dunson DB. Am J Epidemiol 2001, 153:1222–1226.
Bayesian inference of phylogeny and its impact on EVOLUTIONARY
BIOLOGY. Huelsenbeck JP, Ronquist F, Nielsen R, Bollback JP. Science
2001, 294:2310–2314.
Geoadditive Bayesian models for FORESTRY defoliation data: a case
study. Musio, M. and Augustin, N.H. and von Wilpert, K. Environmetrics.
19(6), 630—642, 2008.
Bayesian statistics in GENETICS: a guide for the uninitiated.
Shoemaker, J.S. and Painter, I.S. and Weir, B.S. Trends in Genetics,
15(9), 354-358, 1999.
Bayesian statistics in ONCOLOGY. Adamina, M. and Tomlinson, G. and
Guller, U. Cancer, 115(23), 5371-5381, 2009.
Bayesian analysis in PLANT PATHOLOGY. Mila, AL and Carriquiry, AL.
Phytopathology, 94(9), 1027-1030, 2004.
Bayesian analysis for POLITICAL RESEARCH. Jackman S. Annual Review of
Political Science, 2004, 7:483–505.
The list above could go on and on. The point is simple: Bayesian
methods are being adopted across the disciplines of science. We should
not be laggards in utilizing Bayesian methods in our science, or in
teaching Bayesian methods in our classrooms.
Why are Bayesian methods being adopted across science? Answer:
2. Bayesian methods provide richer information, with greater
flexibility and broader applicability than 20th century methods.
Bayesian methods are intellectually coherent and intuitive. Bayesian
analyses are readily computed with modern software and hardware.
To explain this point adequately would take an entire textbook, but
here are a few highlights.
* In NHST, the data collector must pretend to plan the sample size in
advance and pretend not to let preliminary looks at the data influence
the final sample size. Bayesian design, on the contrary, has no such
pretenses because inference is not based on p values.
* In NHST, analysis of variance (ANOVA) has elaborate corrections for
multiple comparisons based on the intentions of the analyst.
Hierarchical Bayesian ANOVA uses no such corrections, instead rationally
mitigating false alarms based on the data.
* Bayesian computational practice allows easy modification of models
to properly accommodate the measurement scales and distributional needs
of observed data.
* In many NHST analyses, missing data or otherwise unbalanced designs
can produce computational problems. Bayesian models seamlessly handle
unbalanced and small-sample designs.
* In many NHST analyses, individual differences are challenging to
incorporate into the analysis. In hierarchical Bayesian approaches,
individual differences can be flexibly and easily modeled, with
hierarchical priors that provide rational “shrinkage” of individual
estimates.
* In contingency table analysis, the traditional chi-square test
suffers if expected values of cell frequencies are less than 5. There is
no such issue in Bayesian analysis, which handles small or large
frequencies seamlessly.
* In multiple regression analysis, traditional analyses break down
when the predictors are perfectly (or very strongly) correlated, but
Bayesian analysis proceeds as usual and reveals that the estimated
regression coefficients are (anti-)correlated.
* In NHST, the power of an experiment, i.e., the probability of
rejecting the null hypothesis, is based on a single alternative
hypothesis. And the probability of replicating a significant outcome is
“virtually unknowable” according to recent research. But in Bayesian
analysis, both power and replication probability can be computed in
straight forward manner, with the uncertainty of the hypothesis directly
represented.
* Bayesian computational practice allows easy specification of
domain-specific psychometric models in addition to generic models such
as ANOVA and regression.
Some people may have the mistaken impression that the advantages of
Bayesian methods are negated by the need to specify a prior
distribution. In fact, the use of a prior is both appropriate for
rational inference and advantageous in practical applications.
* It is inappropriate not to use a prior. Consider the well known
example of random disease screening. A person is selected at random to
be tested for a rare disease. The test result is positive. What is the
probability that the person actually has the disease? It turns out, even
if the test is highly accurate, the posterior probability of actually
having the disease is surprisingly small. Why? Because the prior
probability of the disease was so small. Thus, incorporating the prior
is crucial for coming to the right conclusion.
* Priors are explicitly specified and must be agreeable to a
skeptical scientific audience. Priors are not capricious and cannot be
covertly manipulated to predetermine a conclusion. If skeptics disagree
with the specification of the prior, then the robustness of the
conclusion can be explicitly examined by considering other reasonable
priors. In most applications, with moderately large data sets and
reasonably informed priors, the conclusions are quite robust.
* Priors are useful for cumulative scientific knowledge and for
leveraging inference from small-sample research. As an empirical domain
matures, more and more data accumulate regarding particular procedures
and outcomes. The accumulated results can inform the priors of
subsequent research, yielding greater precision and firmer conclusions.
* When different groups of scientists have differing priors, stemming
from differing theories and empirical emphases, then Bayesian methods
provide rational means for comparing the conclusions from the different
priors.
To summarize, priors are not a problematic nuisance to be avoided.
Instead, priors should be embraced as appropriate in rational inference
and advantageous in real research.
If those advantages of Bayesian methods are not enough to attract
change, there is also a major reason to be repelled from the dominant
method of the 20th century:
3. 20th century null-hypothesis significance testing (NHST), with its
reliance on p values, has many severe problems. There is little reason
to persist with NHST now that Bayesian methods are accessible to
everyone.
Although there are many difficulties in using p values, the
fundamental fatal flaw of p values is that they are ill defined, because
any set of data has many different p values.
Consider the simple case of assessing whether an electorate prefers
candidate A over candidate B. A quick random poll reveals that 8 people
prefer candidate A out of 23 respondents. What is the p value of that
outcome if the population were equally divided? There is no single
answer! If the pollster intended to stop when N=23, then the p value is
based on repeating an experiment in which N is fixed at 23. If the
pollster intended to stop after the 8th respondent who preferred
candidate A, then the p value is based on repeating an experiment in
which N can be anything from 8 to infinity. If the pollster intended to
poll for one hour, then the p value is based on repeating an experiment
in which N can be anything from zero to infinity. There is a different p
value for every possible intention of the pollster, even though the
observed data are fixed, and even though the outcomes of the queries are
carefully insulated from the intentions of the pollster.
The problem of ill-defined p values is magnified for realistic
situations. In particular, consider the well-known issue of multiple
comparisons in analysis of variance (ANOVA). When there are several
groups, we usually are interested in a variety of comparisons among
them: Is group A significantly different from group B? Is group C
different from group D? Is the average of groups A and B different from
the average of groups C and D? Every comparison presents another
opportunity for a false alarm, i.e., rejecting the null hypothesis when
it is true. Therefore the NHST literature is replete with
recommendations for how to mitigate the “experimentwise” false alarm
rate, using corrections such as Bonferroni, Tukey, Scheffe, etc. The
bizarre part of this practice is that the p value for the single
comparison of groups A and B depends on what other groups you intend to
compare them with. The data in groups A and B are fixed, but merely
intending to compare them with other groups enlarges the p value of the
A vs B comparison. The p value grows because there is a different space
of possible experimental outcomes when the intended experiment comprises
more groups. Therefore it is trivial to make any comparison have a large
p value and be nonsignificant; all you have to do is intend to compare
the data with other groups in the future.
The literature is full of articles pointing out the many conceptual
misunderstandings held by practitioners of NHST. For example, many
people mistake the p value for the probability that the null hypothesis
is true. Even if those misunderstandings could be eradicated, such that
everyone clearly understood what p values really are, the p values would
still be ill defined. Every fixed set of data would still have many
different p values.
To recapitulate: Science is moving to Bayesian methods because of
their many advantages, both practical and intellectual, over 20th
century NHST. It is time that we convert our research and educational
practices to Bayesian data analysis. I hope you will encourage the
change. It’s the right thing to do.
John K. Kruschke, Revised 14 November 2010,
http://www.indiana.edu/~kruschke/
Mean and Median Applet ---
http://mathdl.maa.org/mathDL/47/?pa=content&sa=viewDocument&nodeId=3204
Thank you for sharing Professor Kady Schneiter of Utah State University
This applet consists of two windows, in the first
(the investigate window), the user fills in a grid to create a distribution
of numbers and to investigate the mean and median of the distribution. The
second window (the identify window) enables users to test their knowledge
about the mean and the median. In this window, the applet displays a
hypothetical distribution and an unspecified marker. The user determines
whether the marker indicates the postion of the mean of the distribution,
the median, both, or neither. Two activities intended to facilitate using
the applet to learn about the mean and median are provided.
Above all, Mr. Silver urges forecasters to become
Bayesians. The English mathematician Thomas Bayes used a mathematical rule to
adjust a base probability number in light of new evidence
Book Review of The Signal and the Noise
by Nate Silver
Price: 16.44 at Barnes and Noble
http://www.barnesandnoble.com/w/the-signal-and-the-noise-nate-silver/1111307421?ean=9781594204111
"Telling Lies From Statistics: Forecasters must avoid
overconfidence—and recognize the degree of uncertainty that attends even the
most careful predictions," by Burton G. Malkiel, The Wall Street Journal,
September 24, 2012 ---
http://professional.wsj.com/article/SB10000872396390444554704577644031670158646.html?mod=djemEditorialPage_t&mg=reno64-wsj
It is almost a parlor game, especially as elections
approach—not only the little matter of who will win but also: by how much?
For Nate Silver, however, prediction is more than a game. It is a science,
or something like a science anyway. Mr. Silver is a well-known forecaster
and the founder of the New York Times political blog FiveThirtyEight.com,
which accurately predicted the outcome of the last presidential election.
Before he was a Times blogger, he was known as a careful analyst of (often
widely unreliable) public-opinion polls and, not least, as the man who hit
upon an innovative system for forecasting the performance of Major League
Baseball players. In "The Signal and the Noise," he takes the reader on a
whirlwind tour of the success and failure of predictions in a wide variety
of fields and offers advice about how we might all improve our forecasting
skill.
Mr. Silver reminds us that we live in an era of
"Big Data," with "2.5 quintillion bytes" generated each day. But he strongly
disagrees with the view that the sheer volume of data will make predicting
easier. "Numbers don't speak for themselves," he notes. In fact, we imbue
numbers with meaning, depending on our approach. We often find patterns that
are simply random noise, and many of our predictions fail: "Unless we become
aware of the biases we introduce, the returns to additional information may
be minimal—or diminishing." The trick is to extract the correct signal from
the noisy data. "The signal is the truth," Mr. Silver writes. "The noise is
the distraction."
The first half of Mr. Silver's analysis looks
closely at the success and failure of predictions in clusters of fields
ranging from baseball to politics, poker to chess, epidemiology to stock
markets, and hurricanes to earthquakes. We do well, for example, with
weather forecasts and political predictions but very badly with earthquakes.
Part of the problem is that earthquakes, unlike hurricanes, often occur
without warning. Half of major earthquakes are preceded by no discernible
foreshocks, and periods of increased seismic activity often never result in
a major tremor—a classic example of "noise." Mr. Silver observes that we can
make helpful forecasts of future performance of baseball's position
players—relying principally on "on-base percentage" and "wins above
replacement player"—but we completely missed the 2008 financial crisis. And
we have made egregious errors in predicting the spread of infectious
diseases such as the flu.
In the second half of his analysis, Mr. Silver
suggests a number of methods by which we can improve our ability. The key,
for him, is less a particular mathematical model than a temperament or
"framing" idea. First, he says, it is important to avoid overconfidence, to
recognize the degree of uncertainty that attends even the most careful
forecasts. The best forecasts don't contain specific numerical expectations
but define the future in terms of ranges (the hurricane should pass
somewhere between Tampa and 350 miles west) and probabilities (there is a
70% chance of rain this evening).
Above all, Mr. Silver urges forecasters to become
Bayesians. The English mathematician Thomas Bayes used a mathematical rule
to adjust a base probability number in light of new evidence. To take a
canonical medical example, 1% of 40-year-old women have breast cancer:
Bayes's rule tells us how to factor in new information, such as a
breast-cancer screening test. Studies of such tests reveal that 80% of women
with breast cancer will get positive mammograms, and 9.6% of women without
breast cancer will also get positive mammograms (so-called false positives).
What is the probability that a woman who gets a positive mammogram will in
fact have breast cancer? Most people, including many doctors, greatly
overestimate the probability that the test will give an accurate diagnosis.
The right answer is less than 8%. The result seems counterintuitive unless
you realize that a large number of (40-year-old) women without breast cancer
will get a positive reading. Ignoring the false positives that always exist
with any noisy data set will lead to an inaccurate estimate of the true
probability.
This example and many others are neatly presented
in "The Signal and the Noise." Mr. Silver's breezy style makes even the most
difficult statistical material accessible. What is more, his arguments and
examples are painstakingly researched—the book has 56 pages of densely
printed footnotes. That is not to say that one must always agree with Mr.
Silver's conclusions, however.
Continued in article
Bayesian Probability ---
http://en.wikipedia.org/wiki/Bayesian_probability
Bayesian Inference ---
http://en.wikipedia.org/wiki/Bayesian_inference
Bob Jensen's threads on free online mathematics and statistics tutorials are at
http://www.trinity.edu/rjensen/Bookbob2.htm#050421Mathematics
Multicollinearity ---
http://en.wikipedia.org/wiki/Multicollinearity
Question
When we took econometrics we learned that predictor variable independence was
good and interdependence was bad, especially higher ordered complicated
interdependencies?
"Can You Actually TEST for Multicollinearity?" ---
Click Here
http://davegiles.blogspot.com/2013/06/can-you-actually-test-for.html?utm_source=feedburner&utm_medium=feed&utm_campaign=Feed%3A+blogspot%2FjjOHE+%28Econometrics+Beat%3A+Dave+Giles%27+Blog%29
. . .
Now, let's return to the "problem" of
multicollinearity.
What do we mean by this term, anyway? This turns
out to be the key question!
Multicollinearity is a phenomenon associated with
our particular sample of data when we're trying to estimate a
regression model. Essentially, it's a situation where there is
insufficient information in the sample of data to enable us to
enable us to draw "reliable" inferences about the individual parameters
of the underlying (population) model.
I'll be elaborating more on the "informational content" aspect of this
phenomenon in a follow-up post. Yes, there are various sample measures
that we can compute and report, to help us gauge how severe this data
"problem" may be. But they're not statistical tests, in any sense
of the word
Because multicollinearity is a characteristic of the sample, and
not a characteristic of the population, you should immediately be
suspicious when someone starts talking about "testing for
multicollinearity". Right?
Apparently not everyone gets it!
There's an old paper by Farrar and Glauber (1967) which, on the face of
it might seem to take a different stance. In fact, if you were around
when this paper was published (or if you've bothered to actually read it
carefully), you'll know that this paper makes two contributions. First,
it provides a very sensible discussion of what multicollinearity is all
about. Second, the authors take some well known results from the
statistics literature (notably, by Wishart, 1928; Wilks, 1932; and
Bartlett, 1950) and use them to give "tests" of the hypothesis that the
regressor matrix, X, is orthogonal.
How can this be? Well, there's a simple explanation if you read the
Farrar and Glauber paper carefully, and note what assumptions are made
when they "borrow" the old statistics results. Specifically, there's an
explicit (and necessary) assumption that in the population the X
matrix is random, and that it follows a multivariate normal
distribution.
This assumption is, of course totally at odds with what is usually
assumed in the linear regression model! The "tests" that Farrar and
Glauber gave us aren't really tests of multicollinearity in the
sample. Unfortunately, this point wasn't fully appreciated by
everyone.
There are some sound suggestions in this paper, including looking at the
sample multiple correlations between each regressor, and all of
the other regressors. These, and other sample measures such as
variance inflation factors, are useful from a diagnostic viewpoint, but
they don't constitute tests of "zero multicollinearity".
So, why am I even mentioning the Farrar and Glauber paper now?
Well, I was intrigued to come across some STATA code (Shehata, 2012)
that allows one to implement the Farrar and Glauber "tests". I'm not
sure that this is really very helpful. Indeed, this seems to me to be a
great example of applying someone's results without understanding
(bothering to read?) the assumptions on which they're based!
Be careful out there - and be highly suspicious of strangers bearing
gifts!
References
Shehata, E. A. E., 2012. FGTEST: Stata module to compute
Farrar-Glauber Multicollinearity Chi2, F, t tests.
Wilks, S. S., 1932. Certain generalizations in the analysis of
variance.
Biometrika, 24, 477-494.
Wishart, J., 1928. The generalized product moment distribution
in samples from a multivariate normal population.
Biometrika,
20A, 32-52.
Multicollinearity ---
http://en.wikipedia.org/wiki/Multicollinearity
Detection
of multicollinearity
Indicators that multicollinearity may be present in a model:
- Large changes in the estimated regression coefficients when a
predictor variable is added or deleted
- Insignificant regression coefficients for the affected variables in
the multiple regression, but a rejection of the joint hypothesis that
those coefficients are all zero (using an F-test)
- If a multivariate regression finds an insignificant coefficient of a
particular explanator, yet a
simple linear regression of the explained variable on this
explanatory variable shows its coefficient to be significantly different
from zero, this situation indicates multicollinearity in the
multivariate regression.
- Some authors have suggested a formal detection-tolerance or the
variance inflation factor (VIF) for multicollinearity:
where
 is the coefficient of determination of a regression of explanator j
on all the other explanators. A tolerance of less than 0.20 or 0.10
and/or a VIF of 5 or 10 and above indicates a multicollinearity problem
(but see O'Brien 2007).[1]
is the coefficient of determination of a regression of explanator j
on all the other explanators. A tolerance of less than 0.20 or 0.10
and/or a VIF of 5 or 10 and above indicates a multicollinearity problem
(but see O'Brien 2007).[1]
- Condition Number Test: The standard measure of
ill-conditioning in a matrix is the condition index. It will
indicate that the inversion of the matrix is numerically unstable with
finite-precision numbers ( standard computer floats and doubles ). This
indicates the potential sensitivity of the computed inverse to small
changes in the original matrix. The Condition Number is computed by
finding the square root of (the maximum eigenvalue divided by the
minimum eigenvalue). If the Condition Number is above 30, the regression
is said to have significant multicollinearity.
- Farrar-Glauber Test:[2]
If the variables are found to be orthogonal, there is no
multicollinearity; if the variables are not orthogonal, then
multicollinearity is present.
- Construction of a correlation matrix among the explanatory variables
will yield indications as to the likelihood that any given couplet of
right-hand-side variables are creating multicollinearity problems.
Correlation values (off-diagonal elements) of at least .4 are sometimes
interpreted as indicating a multicollinearity problem.
Consequences of multicollinearity
As mentioned above, one consequence of a high degree of multicollinearity
is that, even if the matrix XTX is invertible, a computer
algorithm may be unsuccessful in obtaining an approximate inverse, and if it
does obtain one it may be numerically inaccurate. But even in the presence
of an accurate XTX matrix, the following consequences arise:
In the presence of multicollinearity, the estimate of one variable's
impact on the dependent variable
 while controlling for the others tends to be less precise than if predictors
were uncorrelated with one another. The usual interpretation of a regression
coefficient is that it provides an estimate of the effect of a one unit
change in an independent variable,
while controlling for the others tends to be less precise than if predictors
were uncorrelated with one another. The usual interpretation of a regression
coefficient is that it provides an estimate of the effect of a one unit
change in an independent variable,
 ,
holding the other variables constant. If
,
holding the other variables constant. If
 is highly correlated with another independent variable,
is highly correlated with another independent variable,
 ,
in the given data set, then we have a set of observations for which
,
in the given data set, then we have a set of observations for which
 and
and
 have a particular linear stochastic relationship. We don't have a set of
observations for which all changes in
have a particular linear stochastic relationship. We don't have a set of
observations for which all changes in
 are independent of changes in
are independent of changes in
 ,
so we have an imprecise estimate of the effect of independent changes in
,
so we have an imprecise estimate of the effect of independent changes in
 .
.
In some sense, the collinear variables contain the same information about
the dependent variable. If nominally "different" measures actually quantify
the same phenomenon then they are redundant. Alternatively, if the variables
are accorded different names and perhaps employ different numeric
measurement scales but are highly correlated with each other, then they
suffer from redundancy.
One of the features of multicollinearity is that the standard errors of
the affected coefficients tend to be large. In that case, the test of the
hypothesis that the coefficient is equal to zero may lead to a failure to
reject a false null hypothesis of no effect of the explanator.
A principal danger of such data redundancy is that of
overfitting in
regression analysis models. The best regression models are those in
which the predictor variables each correlate highly with the dependent
(outcome) variable but correlate at most only minimally with each other.
Such a model is often called "low noise" and will be statistically robust
(that is, it will predict reliably across numerous samples of variable sets
drawn from the same statistical population).
So long as the underlying specification is correct, multicollinearity
does not actually bias results; it just produces large
standard errors in the related independent variables. If, however, there
are other problems (such as omitted variables) which introduce bias,
multicollinearity can multiply (by orders of magnitude) the effects of that
bias.[citation
needed] More importantly, the usual use of regression
is to take coefficients from the model and then apply them to other data. If
the pattern of multicollinearity in the new data differs from that in the
data that was fitted, such extrapolation may introduce large errors in the
predictions.[3]
Remedies
for multicollinearity
- Make sure you have not fallen into the
dummy variable trap; including a dummy variable for every category
(e.g., summer, autumn, winter, and spring) and including a constant term
in the regression together guarantee perfect multicollinearity.
- Try seeing what happens if you use independent subsets of your data
for estimation and apply those estimates to the whole data set.
Theoretically you should obtain somewhat higher variance from the
smaller datasets used for estimation, but the expectation of the
coefficient values should be the same. Naturally, the observed
coefficient values will vary, but look at how much they vary.
- Leave the model as is, despite multicollinearity. The presence of
multicollinearity doesn't affect the efficacy of extrapolating the
fitted model to new data provided that the predictor variables follow
the same pattern of multicollinearity in the new data as in the data on
which the regression model is based.[4]
- Drop one of the variables. An explanatory variable may be dropped to
produce a model with significant coefficients. However, you lose
information (because you've dropped a variable). Omission of a relevant
variable results in biased coefficient estimates for the remaining
explanatory variables.
- Obtain more data, if possible. This is the preferred solution. More
data can produce more precise parameter estimates (with lower standard
errors), as seen from the formula in
variance inflation factor for the variance of the estimate of a
regression coefficient in terms of the sample size and the degree of
multicollinearity.
- Mean-center the predictor variables. Generating polynomial terms
(i.e., for
 ,
,
 ,
,
 ,
etc.) can cause some multicolinearity if the variable in question has a
limited range (e.g., [2,4]). Mean-centering will eliminate this special
kind of multicollinearity. However, in general, this has no effect. It
can be useful in overcoming problems arising from rounding and other
computational steps if a carefully designed computer program is not
used.
,
etc.) can cause some multicolinearity if the variable in question has a
limited range (e.g., [2,4]). Mean-centering will eliminate this special
kind of multicollinearity. However, in general, this has no effect. It
can be useful in overcoming problems arising from rounding and other
computational steps if a carefully designed computer program is not
used.
- Standardize your independent variables. This may help reduce a false
flagging of a condition index above 30.
- It has also been suggested that using the
Shapley value, a game theory tool, the model could account for the
effects of multicollinearity. The Shapley value assigns a value for each
predictor and assesses all possible combinations of importance.[5]
-
Ridge regression or
principal component regression can be used.
- If the correlated explanators are different lagged values of the
same underlying explanator, then a
distributed lag technique can be used, imposing a general structure
on the relative values of the coefficients to be estimated.
Note that one technique that does not work in offsetting the effects of
multicollinearity is
orthogonalizing the explanatory variables (linearly transforming them so
that the transformed variables are uncorrelated with each other): By the
Frisch–Waugh–Lovell theorem, using projection matrices to make the
explanatory variables orthogonal to each other will lead to the same results
as running the regression with all non-orthogonal explanators included.
Examples of contexts in which multicollinearity arises
Survival analysis
Multicollinearity may represent a serious issue in
survival analysis. The problem is that time-varying covariates may
change their value over the time line of the study. A special procedure is
recommended to assess the impact of multicollinearity on the results. See
Van den Poel & Larivière (2004)[6]
for a detailed discussion.
Interest rates for different terms to maturity
In various situations it might be hypothesized that multiple interest
rates of various terms to maturity all influence some economic decision,
such as the amount of money or some other financial asset to hold, or the
amount of fixed investment spending to engage in. In this case, including
these various interest rates will in general create a substantial
multicollinearity problem because interest rates tend to move together. If
in fact each of the interest rates has its own separate effect on the
dependent variable, it can be extremely difficult to separate out their
effects.
Bob Jensen's threads on the differences between the science and pseudo
science ---
http://www.cs.trinity.edu/~rjensen/temp/AccounticsDamn.htm#Pseudo-Science
Simpson's Paradox and Cross-Validation
Simpson's Paradox ---
http://en.wikipedia.org/wiki/Simpson%27s_paradox
"Simpson’s Paradox: A Cautionary Tale in Advanced Analytics," by Steve
Berman, Leandro DalleMule, Michael Greene, and John Lucker, Significance:
Statistics Making Sense, October 2012 ---
http://www.significancemagazine.org/details/webexclusive/2671151/Simpsons-Paradox-A-Cautionary-Tale-in-Advanced-Analytics.html
Analytics projects often present us with situations
in which common sense tells us one thing, while the numbers seem to tell us
something much different. Such situations are often opportunities to learn
something new by taking a deeper look at the data. Failure to perform a
sufficiently nuanced analysis, however, can lead to misunderstandings and
decision traps. To illustrate this danger, we present several instances of
Simpson’s Paradox in business and non-business environments. As we
demonstrate below, statistical tests and analysis can be confounded by a
simple misunderstanding of the data. Often taught in elementary probability
classes, Simpson’s Paradox refers to situations in which a trend or
relationship that is observed within multiple groups reverses when the
groups are combined. Our first example describes how Simpson’s Paradox
accounts for a highly surprising observation in a healthcare study. Our
second example involves an apparent violation of the law of supply and
demand: we describe a situation in which price changes seem to bear no
relationship with quantity purchased. This counterintuitive relationship,
however, disappears once we break the data into finer time periods. Our
final example illustrates how a naive analysis of marginal profit
improvements resulting from a price optimization project can potentially
mislead senior business management, leading to incorrect conclusions and
inappropriate decisions. Mathematically, Simpson’s Paradox is a fairly
simple—if counterintuitive—arithmetic phenomenon. Yet its significance for
business analytics is quite far-reaching. Simpson’s Paradox vividly
illustrates why business analytics must not be viewed as a purely technical
subject appropriate for mechanization or automation. Tacit knowledge, domain
expertise, common sense, and above all critical thinking, are necessary if
analytics projects are to reliably lead to appropriate evidence-based
decision making.
The past several years have seen decision making in
many areas of business steadily evolve from judgment-driven domains into
scientific domains in which the analysis of data and careful consideration
of evidence are more prominent than ever before. Additionally, mainstream
books, movies, alternative media and newspapers have covered many topics
describing how fact and metric driven analysis and subsequent action can
exceed results previously achieved through less rigorous methods. This trend
has been driven in part by the explosive growth of data availability
resulting from Enterprise Resource Planning (ERP) and Customer Relationship
Management (CRM) applications and the Internet and eCommerce more generally.
There are estimates that predict that more data will be created in the next
four years than in the history of the planet. For example, Wal-Mart handles
over one million customer transactions every hour, feeding databases
estimated at more than 2.5 petabytes in size - the equivalent of 167 times
the books in the United States Library of Congress.
Additionally, computing power has increased
exponentially over the past 30 years and this trend is expected to continue.
In 1969, astronauts landed on the moon with a 32-kilobyte memory computer.
Today, the average personal computer has more computing power than the
entire U.S. space program at that time. Decoding the human genome took 10
years when it was first done in 2003; now the same task can be performed in
a week or less. Finally, a large consumer credit card issuer crunched two
years of data (73 billion transactions) in 13 minutes, which not long ago
took over one month.
This explosion of data availability and the
advances in computing power and processing tools and software have paved the
way for statistical modeling to be at the front and center of decision
making not just in business, but everywhere. Statistics is the means to
interpret data and transform vast amounts of raw data into meaningful
information.
However, paradoxes and fallacies lurk behind even
elementary statistical exercises, with the important implication that
exercises in business analytics can produce deceptive results if not
performed properly. This point can be neatly illustrated by pointing to
instances of Simpson’s Paradox. The phenomenon is named after Edward
Simpson, who described it in a technical paper in the 1950s, though the
prominent statisticians Karl Pearson and Udney Yule noticed the phenomenon
over a century ago. Simpson’s Paradox, which regularly crops up in
statistical research, business analytics, and public policy, is a prime
example of why statistical analysis is useful as a corrective for the many
ways in which humans intuit false patterns in complex datasets.
Simpson’s Paradox is in a sense an arithmetic
trick: weighted averages can lead to reversals of meaningful
relationships—i.e., a trend or relationship that is observed within each of
several groups reverses when the groups are combined. Simpson’s Paradox can
arise in any number of marketing and pricing scenarios; we present here case
studies describing three such examples. These case studies serve as
cautionary tales: there is no comprehensive mechanical way to detect or
guard against instances of Simpson’s Paradox leading us astray. To be
effective, analytics projects should be informed by both a nuanced
understanding of statistical methodology as well as a pragmatic
understanding of the business being analyzed.
The first case study, from the medical field,
presents a surface indication on the effects of smoking that is at odds with
common sense. Only when the data are viewed at a more refined level of
analysis does one see the true effects of smoking on mortality. In the
second case study, decreasing prices appear to be associated with decreasing
sales and increasing prices appear to be associated with increasing sales.
On the surface, this makes no sense. A fundamental tenet of economics is
that of the demand curve: as the price of a good or service increases,
consumers demand less of it. Simpson’s Paradox is responsible for an
apparent—though illusory—violation of this fundamental law of economics. Our
final case study shows how marginal improvements in profitability in each of
the sales channels of a given manufacturer may result in an apparent
marginal reduction in the overall profitability the business. This seemingly
contradictory conclusion can also lead to serious decision traps if not
properly understood.
Case Study 1: Are those warning labels
really necessary?
We start with a simple example from the healthcare
world. This example both illustrates the phenomenon and serves as a reminder
that it can appear in any domain.
The data are taken from a 1996 follow-up study from
Appleton, French, and Vanderpump on the effects of smoking. The follow-up
catalogued women from the original study, categorizing based on the age
groups in the original study, as well as whether the women were smokers or
not. The study measured the deaths of smokers and non-smokers during the 20
year period.
Continued in article
What happened to cross-validation in
accountics science research?
Over time I've become increasingly critical of
the lack of validation in accountics science, and I've focused mainly upon lack
of replication by independent researchers and lack of commentaries published in
accountics science journals ---
http://www.trinity.edu/rjensen/TheoryTAR.htm
Another type of validation that seems to be on
the decline in accountics science are the so-called cross-validations.
Accountics scientists seem to be content with their statistical inference tests
on Z-Scores, F-Tests, and correlation significance testing. Cross-validation
seems to be less common, at least I'm having troubles finding examples of
cross-validation. Cross-validation entails comparing sample findings with
findings in holdout samples.
Cross Validation ---
http://en.wikipedia.org/wiki/Cross-validation_%28statistics%29
When reading the following paper using logit
regression to to predict audit firm changes, it struck me that this would've
been an ideal candidate for the authors to have performed cross-validation using
holdout samples.
"Audit Quality and Auditor Reputation: Evidence from Japan," by Douglas J.
Skinner and Suraj Srinivasan, The Accounting Review, September 2012, Vol.
87, No. 5, pp. 1737-1765.
We study events surrounding
ChuoAoyama's failed audit of Kanebo, a large Japanese cosmetics company
whose management engaged in a massive accounting fraud. ChuoAoyama was PwC's
Japanese affiliate and one of Japan's largest audit firms. In May 2006, the
Japanese Financial Services Agency (FSA) suspended ChuoAoyama for two months
for its role in the Kanebo fraud. This unprecedented action followed a
series of events that seriously damaged ChuoAoyama's reputation. We use
these events to provide evidence on the importance of auditors' reputation
for quality in a setting where litigation plays essentially no role. Around
one quarter of ChuoAoyama's clients defected from the firm after its
suspension, consistent with the importance of reputation. Larger firms and
those with greater growth options were more likely to leave, also consistent
with the reputation argument.
Jensen Comment
Rather than just use statistical inference tests
on logit model Z-statistics, it struck me that in statistics journals the
referees might've requested cross-validation tests on holdout samples of firms
that changed auditors and firms that did not change auditors.
I do find somewhat more frequent
cross-validation studies in finance, particularly in the areas of discriminant
analysis in bankruptcy prediction modes.
Instances of cross-validation in accounting
research journals seem to have died out in the past 20 years. There are earlier
examples of cross-validation in accounting research journals. Several examples
are cited below:
"A field study examination of budgetary
participation and locus of control," by Peter Brownell, The Accounting
Review, October 1982 ---
http://www.jstor.org/discover/10.2307/247411?uid=3739712&uid=2&uid=4&uid=3739256&sid=21101146090203
"Information choice and utilization in an
experiment on default prediction," Abdel-Khalik and KM El-Sheshai -
Journal of Accounting Research, 1980 ---
http://www.jstor.org/discover/10.2307/2490581?uid=3739712&uid=2&uid=4&uid=3739256&sid=21101146090203
"Accounting ratios and the prediction of
failure: Some behavioral evidence," by Robert Libby, Journal of
Accounting Research, Spring 1975 ---
http://www.jstor.org/discover/10.2307/2490653?uid=3739712&uid=2&uid=4&uid=3739256&sid=21101146090203
There are other examples of cross-validation
in the 1970s and 1980s, particularly in bankruptcy prediction.
I have trouble finding illustrations of
cross-validation in the accounting research literature in more recent years. Has
the interest in cross-validating waned along with interest in validating
accountics research? Or am I just being careless in my search for illustrations?
Simpson's Paradox and Cross-Validation
Simpson's Paradox ---
http://en.wikipedia.org/wiki/Simpson%27s_paradox
"Simpson’s Paradox: A Cautionary Tale in Advanced Analytics," by Steve
Berman, Leandro DalleMule, Michael Greene, and John Lucker, Significance:
Statistics Making Sense, October 2012 ---
http://www.significancemagazine.org/details/webexclusive/2671151/Simpsons-Paradox-A-Cautionary-Tale-in-Advanced-Analytics.html
Analytics projects often present us with situations
in which common sense tells us one thing, while the numbers seem to tell us
something much different. Such situations are often opportunities to learn
something new by taking a deeper look at the data. Failure to perform a
sufficiently nuanced analysis, however, can lead to misunderstandings and
decision traps. To illustrate this danger, we present several instances of
Simpson’s Paradox in business and non-business environments. As we
demonstrate below, statistical tests and analysis can be confounded by a
simple misunderstanding of the data. Often taught in elementary probability
classes, Simpson’s Paradox refers to situations in which a trend or
relationship that is observed within multiple groups reverses when the
groups are combined. Our first example describes how Simpson’s Paradox
accounts for a highly surprising observation in a healthcare study. Our
second example involves an apparent violation of the law of supply and
demand: we describe a situation in which price changes seem to bear no
relationship with quantity purchased. This counterintuitive relationship,
however, disappears once we break the data into finer time periods. Our
final example illustrates how a naive analysis of marginal profit
improvements resulting from a price optimization project can potentially
mislead senior business management, leading to incorrect conclusions and
inappropriate decisions. Mathematically, Simpson’s Paradox is a fairly
simple—if counterintuitive—arithmetic phenomenon. Yet its significance for
business analytics is quite far-reaching. Simpson’s Paradox vividly
illustrates why business analytics must not be viewed as a purely technical
subject appropriate for mechanization or automation. Tacit knowledge, domain
expertise, common sense, and above all critical thinking, are necessary if
analytics projects are to reliably lead to appropriate evidence-based
decision making.
The past several years have seen decision making in
many areas of business steadily evolve from judgment-driven domains into
scientific domains in which the analysis of data and careful consideration
of evidence are more prominent than ever before. Additionally, mainstream
books, movies, alternative media and newspapers have covered many topics
describing how fact and metric driven analysis and subsequent action can
exceed results previously achieved through less rigorous methods. This trend
has been driven in part by the explosive growth of data availability
resulting from Enterprise Resource Planning (ERP) and Customer Relationship
Management (CRM) applications and the Internet and eCommerce more generally.
There are estimates that predict that more data will be created in the next
four years than in the history of the planet. For example, Wal-Mart handles
over one million customer transactions every hour, feeding databases
estimated at more than 2.5 petabytes in size - the equivalent of 167 times
the books in the United States Library of Congress.
Additionally, computing power has increased
exponentially over the past 30 years and this trend is expected to continue.
In 1969, astronauts landed on the moon with a 32-kilobyte memory computer.
Today, the average personal computer has more computing power than the
entire U.S. space program at that time. Decoding the human genome took 10
years when it was first done in 2003; now the same task can be performed in
a week or less. Finally, a large consumer credit card issuer crunched two
years of data (73 billion transactions) in 13 minutes, which not long ago
took over one month.
This explosion of data availability and the
advances in computing power and processing tools and software have paved the
way for statistical modeling to be at the front and center of decision
making not just in business, but everywhere. Statistics is the means to
interpret data and transform vast amounts of raw data into meaningful
information.
However, paradoxes and fallacies lurk behind even
elementary statistical exercises, with the important implication that
exercises in business analytics can produce deceptive results if not
performed properly. This point can be neatly illustrated by pointing to
instances of Simpson’s Paradox. The phenomenon is named after Edward
Simpson, who described it in a technical paper in the 1950s, though the
prominent statisticians Karl Pearson and Udney Yule noticed the phenomenon
over a century ago. Simpson’s Paradox, which regularly crops up in
statistical research, business analytics, and public policy, is a prime
example of why statistical analysis is useful as a corrective for the many
ways in which humans intuit false patterns in complex datasets.
Simpson’s Paradox is in a sense an arithmetic
trick: weighted averages can lead to reversals of meaningful
relationships—i.e., a trend or relationship that is observed within each of
several groups reverses when the groups are combined. Simpson’s Paradox can
arise in any number of marketing and pricing scenarios; we present here case
studies describing three such examples. These case studies serve as
cautionary tales: there is no comprehensive mechanical way to detect or
guard against instances of Simpson’s Paradox leading us astray. To be
effective, analytics projects should be informed by both a nuanced
understanding of statistical methodology as well as a pragmatic
understanding of the business being analyzed.
The first case study, from the medical field,
presents a surface indication on the effects of smoking that is at odds with
common sense. Only when the data are viewed at a more refined level of
analysis does one see the true effects of smoking on mortality. In the
second case study, decreasing prices appear to be associated with decreasing
sales and increasing prices appear to be associated with increasing sales.
On the surface, this makes no sense. A fundamental tenet of economics is
that of the demand curve: as the price of a good or service increases,
consumers demand less of it. Simpson’s Paradox is responsible for an
apparent—though illusory—violation of this fundamental law of economics. Our
final case study shows how marginal improvements in profitability in each of
the sales channels of a given manufacturer may result in an apparent
marginal reduction in the overall profitability the business. This seemingly
contradictory conclusion can also lead to serious decision traps if not
properly understood.
Case Study 1: Are those warning labels
really necessary?
We start with a simple example from the healthcare
world. This example both illustrates the phenomenon and serves as a reminder
that it can appear in any domain.
The data are taken from a 1996 follow-up study from
Appleton, French, and Vanderpump on the effects of smoking. The follow-up
catalogued women from the original study, categorizing based on the age
groups in the original study, as well as whether the women were smokers or
not. The study measured the deaths of smokers and non-smokers during the 20
year period.
Continued in article
What happened to cross-validation in
accountics science research?
Over time I've become increasingly critical of
the lack of validation in accountics science, and I've focused mainly upon lack
of replication by independent researchers and lack of commentaries published in
accountics science journals ---
http://www.trinity.edu/rjensen/TheoryTAR.htm
Another type of validation that seems to be on
the decline in accountics science are the so-called cross-validations.
Accountics scientists seem to be content with their statistical inference tests
on Z-Scores, F-Tests, and correlation significance testing. Cross-validation
seems to be less common, at least I'm having troubles finding examples of
cross-validation. Cross-validation entails comparing sample findings with
findings in holdout samples.
Cross Validation ---
http://en.wikipedia.org/wiki/Cross-validation_%28statistics%29
When reading the following paper using logit
regression to to predict audit firm changes, it struck me that this would've
been an ideal candidate for the authors to have performed cross-validation using
holdout samples.
"Audit Quality and Auditor Reputation: Evidence from Japan," by Douglas J.
Skinner and Suraj Srinivasan, The Accounting Review, September 2012, Vol.
87, No. 5, pp. 1737-1765.
We study events surrounding
ChuoAoyama's failed audit of Kanebo, a large Japanese cosmetics company
whose management engaged in a massive accounting fraud. ChuoAoyama was PwC's
Japanese affiliate and one of Japan's largest audit firms. In May 2006, the
Japanese Financial Services Agency (FSA) suspended ChuoAoyama for two months
for its role in the Kanebo fraud. This unprecedented action followed a
series of events that seriously damaged ChuoAoyama's reputation. We use
these events to provide evidence on the importance of auditors' reputation
for quality in a setting where litigation plays essentially no role. Around
one quarter of ChuoAoyama's clients defected from the firm after its
suspension, consistent with the importance of reputation. Larger firms and
those with greater growth options were more likely to leave, also consistent
with the reputation argument.
Jensen Comment
Rather than just use statistical inference tests
on logit model Z-statistics, it struck me that in statistics journals the
referees might've requested cross-validation tests on holdout samples of firms
that changed auditors and firms that did not change auditors.
I do find somewhat more frequent
cross-validation studies in finance, particularly in the areas of discriminant
analysis in bankruptcy prediction modes.
Instances of cross-validation in accounting
research journals seem to have died out in the past 20 years. There are earlier
examples of cross-validation in accounting research journals. Several examples
are cited below:
"A field study examination of budgetary
participation and locus of control," by Peter Brownell, The Accounting
Review, October 1982 ---
http://www.jstor.org/discover/10.2307/247411?uid=3739712&uid=2&uid=4&uid=3739256&sid=21101146090203
"Information choice and utilization in an
experiment on default prediction," Abdel-Khalik and KM El-Sheshai -
Journal of Accounting Research, 1980 ---
http://www.jstor.org/discover/10.2307/2490581?uid=3739712&uid=2&uid=4&uid=3739256&sid=21101146090203
"Accounting ratios and the prediction of
failure: Some behavioral evidence," by Robert Libby, Journal of
Accounting Research, Spring 1975 ---
http://www.jstor.org/discover/10.2307/2490653?uid=3739712&uid=2&uid=4&uid=3739256&sid=21101146090203
There are other examples of cross-validation
in the 1970s and 1980s, particularly in bankruptcy prediction.
I have trouble finding illustrations of
cross-validation in the accounting research literature in more recent years. Has
the interest in cross-validating waned along with interest in validating
accountics research? Or am I just being careless in my search for illustrations?
) has
reminded us that if the sample size is sufficiently large, then it's
virtually impossible not to reject almost any hypothesis.
So, if the sample is very large and the p-values associated with
the estimated coefficients in a regression model are of the order of, say,
0.10 or even 0.05, then this really bad news. Much,
much, smaller p-values are needed before we get all excited about
'statistically significant' results when the sample size is in the
thousands, or even bigger. So, the p-values reported above are
mostly pretty marginal, as far as significance is concerned. When you work
out the p-values for the other 6 models I mentioned, they range
from to 0.005 to 0.460. I've been generous in the models I selected.


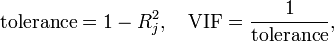
 is the coefficient of determination of a regression of explanator j
on all the other explanators. A tolerance of less than 0.20 or 0.10
and/or a VIF of 5 or 10 and above indicates a multicollinearity problem
(but see O'Brien 2007).
is the coefficient of determination of a regression of explanator j
on all the other explanators. A tolerance of less than 0.20 or 0.10
and/or a VIF of 5 or 10 and above indicates a multicollinearity problem
(but see O'Brien 2007). while controlling for the others tends to be less precise than if predictors
were uncorrelated with one another. The usual interpretation of a regression
coefficient is that it provides an estimate of the effect of a one unit
change in an independent variable,
while controlling for the others tends to be less precise than if predictors
were uncorrelated with one another. The usual interpretation of a regression
coefficient is that it provides an estimate of the effect of a one unit
change in an independent variable,
 ,
holding the other variables constant. If
,
holding the other variables constant. If
 ,
in the given data set, then we have a set of observations for which
,
in the given data set, then we have a set of observations for which
 ,
,
 ,
,
 ,
etc.) can cause some multicolinearity if the variable in question has a
limited range (e.g., [2,4]). Mean-centering will eliminate this special
kind of multicollinearity. However, in general, this has no effect. It
can be useful in overcoming problems arising from rounding and other
computational steps if a carefully designed computer program is not
used.
,
etc.) can cause some multicolinearity if the variable in question has a
limited range (e.g., [2,4]). Mean-centering will eliminate this special
kind of multicollinearity. However, in general, this has no effect. It
can be useful in overcoming problems arising from rounding and other
computational steps if a carefully designed computer program is not
used.